Курсовая работа: Фазовые равновесия
Курсовая работа: Фазовые равновесия
Федеральное агентство по образованию
Астраханский Государственный Университет
Кафедра Аналитической и
Физической химии
Курсовая
Фазовые равновесия
Выполнила
Студентка группы ДХМ 311
Шамаева Амина
Проверила
к.х.н. доцент Джигола Л.А.
Астрахань 2008 год
Содержание
Введение
2. Правило фаз Гиббса
3. Равновесные состояния при фазовых переходах
3.1 Равновесие газ – жидкий раствор в двухкомпонентных системах
3.1.1 Зависимость растворимости газов в жидкостях от природы газа и растворителя
3.1.2 Зависимость растворимости газов в жидкостях от давления
3.1.3 Зависимость растворимости газов в жидкостях от температуры
3.2 Равновесие жидкость – жидкость в двухкомпонентных системах
3.3 Равновесие пар – жидкий раствор в двухкомпонентных системах
3.3.1 Равновесие пар—жидкий раствор в системах с неограниченной взаимной растворимостью жидкостей
3.3.2 Равновесие пар — жидкий раствор в системах с ограниченной взаимной растворимостью жидкостей
3.3.3 Равновесие пар—жидкий раствор в системах с взаимно нерастворимыми жидкостями
4. Уравнение Клапейрона
5. Уравнение Клаузиуса – Клапейрона
6. Практическая часть
6.1 Вопросы
6.2 Задачи
Заключение
Библиографический список
Введение
Гетерогенная система - система, состоящая из нескольких фаз.
Фазой называется совокупность гомогенных (однородных) частей системы, одинаковых по составу, химическим и физическим свойствам и отграниченных от других частей системы поверхностью. Поверхности раздела фаз образуются некоторым количеством молекул, расположенных на границе области, заполненной данной фазой. Молекулы, образующие поверхностный слой, находятся в особых условиях, вследствие чего поверхностный слой обладает особыми свойствами, не присущими веществу, находящемуся в глубине фазы. Образования, составленные из небольшого числа молекул, не могут быть разделены на поверхностный слой и внутреннюю массу вещества, поэтому к образованиям с очень малым объемом понятие фаза неприменимо. Жидкие и твердые фазы называются конденсированными.
Составляющее вещество системы - это каждое вещество системы, которое может быть выделено из системы и существовать вне ее. Если в системе не протекает химическая реакция, то количество каждого из веществ не зависит от количеств других веществ. Если в системе протекает химическая реакция, то состав фаз равновесной системы можно определить, зная концентрацию только части веществ. Составляющие вещества, концентрации которых определяют состав фаз данной равновесной системы, называют независимыми составляющими веществами или компонентами системы. Свойства системы определяются не только природой компонентов, но и их числом. Число компонентов совпадает с числом составляющих веществ при отсутствии химической реакции или меньше при наличии химической реакции.
| Система | Число составляющих веществ | Число компонентов |
|
Система состоит из H2(г), J2(г), HJ(г); Возможна реакция: H2(г) + J2(г) = 2 HJ(г) Система состоит из СаСО3, СаО,СО2 Возможна реакция: СаСО3(т) = СаО(т) + СО2(г) Система состоит из Н2, Не, Аr; Нет химического взаимодействия |
3 3 3 3 3 3 3 |
2 2 2 2 3 3 3 |
2. Правило фаз Гиббса
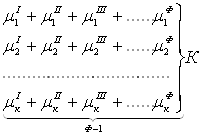
В равновесной системе связь между числами фаз, компонентов и термодинамических степеней свободы выражается правилом фаз Гиббса или законом равновесия фаз. Рассмотрим равновесную термодинамическую систему, состоящую из Ф фаз, каждая из которых содержит К компонентов. Примем в качестве параметров, определяющих состояние системы, давление, температуру и концентрации компонентов, выраженные в массовых или молярных долях или процентах. Оценим общее число параметров состояния и число уравнений, связывающих их. Число параметров, одинаковых во всех фазах системы, равно двум (Р и Т). Поскольку концентрации компонентов выражены в массовых или молярных долях или процентах, то для характеристики состава одной фазы достаточно задать (К — 1) концентраций. Концентрация одного из компонентов данной фазы будет определена, если известны концентрации остальных компонентов. Для характеристики состава всех фаз равновесной системы необходимо знать Ф(К — 1) концентраций. Тогда общее число параметров, определяющих состояние равновесной системы, будет равно Ф(К — 1) + 2.
Так как при Р
= соnst T=const химические потенциалы компонентов являются функциями их
концентраций, например, в идеальном растворе![]() , то число уравнений, связывающих
концентрации компонентов равновесной системы, можно определить из равенства
химических потенциалов каждого компонента во всех фазах :
, то число уравнений, связывающих
концентрации компонентов равновесной системы, можно определить из равенства
химических потенциалов каждого компонента во всех фазах :
 (1)
(1)
Число уравнений, связывающих концентрации одного компонента, равно (Ф — 1), а всех К компонентов — К(Ф — 1). Число независимых параметров состояния системы, т.е. число термодинамических степеней свободы, равно разности между общим числом параметров, определяющих состояние равновесной системы, и числом уравнений, связывающих эти параметры:
С = Ф(К - 1) + 2 - К(Ф - 1),
С=К-Ф + 2. (2)
Уравнение (2) называется правилом фаз Гиббса или законом равновесия фаз: в равновесной термодинамической системе, на которую из внешних факторов оказывают влияние только давление и температура. Число термодинамических степеней свободы равно числу компонентов минус число фаз плюс два. Число степеней свободы возрастает с увеличением числа компонентов и уменьшается с увеличением числа фаз. Поскольку число степеней свободы не может быть отрицательным, число фаз в равновесной системе не может превышать К + 2.
Правило фаз было выведено американским физиком Дж. Гиббсом в 1876 г. Учение о фазах в дальнейшем было использовано в работах Я. Вант-Гоффа, Б. Розебома, Н.С. Курнакова и др. и явилось основой изучения равновесий в гетерогенных системах. Если из внешних факторов на систему оказывает влияние только давление (Р=соnst) или температура (T=const), число степеней свободы уменьшается на единицу и уравнение правила фаз (2) принимает вид
СуСЛ = К-Ф+1 (3)
Вариантность системы, рассчитанная по этому уравнению, называется условной (Сусл), а система — условно инвариантной, условно моновариантной и т.д. При постоянстве давления и температуры
Cусл=К-Ф (4)
Если составы двух равновесных фаз, например жидкой и парообразной, одинаковы, то при подсчете числа степеней свободы следует учитывать еще одно уравнение, связывающее концентрации компонентов Х,(ж) = Х,(п). В этом случае вместо уравнения (2) следует пользоваться уравнением
СуСЛ = К-Ф+1 (5)
а вместо уравнения (3) — уравнением
Cусл=К-Ф (6)
Если состояние системы определяется и такими внешними факторами, как электрическое или магнитное поле, поле тяготения и др., то их также следует учитывать при подсчете числа степеней свободы в равновесной системе. В общем случае, когда на систему действуют п различных факторов, то
С=К-Ф+n (7)
3. Равновесные состояния при фазовых переходах
3.1 Равновесие газ—жидкий раствор в двухкомпонентных системах
При
растворении газов в жидкостях устанавливается равновесие между жидкой фазой,
содержащей растворитель и растворенный газ, и газовой фазой, содержащей данный
газ и пары растворителя. Если растворитель относительно мало летуч, то
установится равновесие между раствором и практически чистым растворяемым газом.
Растворимость вещества определяется его концентрацией в насыщенном растворе. Растворимость
газов в жидкостях зависит от природы растворяемого газа и растворителя,
давления газа, температуры и от присутствия в растворе различных веществ,
особенно электролитов. Числовое значение растворимости газа в жидкости зависит
от способа ее выражения. Растворимость газов выражают числом граммов газа в 100
г чистого растворителя или в 100 г раствора, числом молей газа в 1000 г
растворителя или в 1 л раствора, молярной долей. Кроме того, растворимость
газов в жидкостях характеризуют коэффициентом растворимости о или коэффициентом
поглощения ![]() .
Коэффициент растворимости равен объему газа, выраженному в кубических метрах,
растворенному в 1 м3 растворителя при данной температуре и
приведенному к давлению
.
Коэффициент растворимости равен объему газа, выраженному в кубических метрах,
растворенному в 1 м3 растворителя при данной температуре и
приведенному к давлению ![]() Па (1 атм). Коэффициент
поглощения равен объему газа, выраженному в кубических метрах, растворенному в
1 м3 растворителя и приведенному к Р=
Па (1 атм). Коэффициент
поглощения равен объему газа, выраженному в кубических метрах, растворенному в
1 м3 растворителя и приведенному к Р= ![]() Па (1 атм) и Т= 273
К. Отсюда
Па (1 атм) и Т= 273
К. Отсюда ![]()
3.1.1 Зависимость растворимости газов в жидкостях от природы газа и растворителя
Растворимость
различных газов в одном и том же растворителе при одинаковых условиях
изменяется в очень широких пределах. Растворимость газов повышается при химическом
взаимодействии растворяемого газа с растворителем. На растворимость газов в
жидкостях оказывает влияние и природа растворителя. Если растворители относятся
к одному и тому же классу соединений, то растворимость газа часто мало зависит
от индивидуальных свойств растворителя. В присутствии электролитов
растворимость газов в жидкостях уменьшается. Так, при 298 К и ![]() Па в 1 м3
воды растворяется 0,01915 м3 водорода, а в 1 м3 3н NaОН — 0,0072 м3.
Влияние электролитов на растворимость газов в водных растворах описывается
уравнением И.М.Сеченова:
Па в 1 м3
воды растворяется 0,01915 м3 водорода, а в 1 м3 3н NaОН — 0,0072 м3.
Влияние электролитов на растворимость газов в водных растворах описывается
уравнением И.М.Сеченова:
![]()
где![]() и
и ![]() — растворимость
газа в воде и в растворе электролита соответственно; k — постоянная,
характерная для данного электролита; с — концентрация электролита,
моль/л. Уменьшение растворимости газов в присутствии солей называется
высаливанием. Высаливающее действие иона повышается с ростом заряда и
уменьшается с увеличением радиуса иона. Уменьшение растворимости газов в
присутствии электролитов объясняется в основном тем, что ионы притягивают
молекулы воды и не притягивают неполярные и слабо поляризуемые молекулы газов,
вследствие чего увеличивается фугитивность растворенного газа.
— растворимость
газа в воде и в растворе электролита соответственно; k — постоянная,
характерная для данного электролита; с — концентрация электролита,
моль/л. Уменьшение растворимости газов в присутствии солей называется
высаливанием. Высаливающее действие иона повышается с ростом заряда и
уменьшается с увеличением радиуса иона. Уменьшение растворимости газов в
присутствии электролитов объясняется в основном тем, что ионы притягивают
молекулы воды и не притягивают неполярные и слабо поляризуемые молекулы газов,
вследствие чего увеличивается фугитивность растворенного газа.
3.1.2 Зависимость растворимости газов в жидкостях от давления
Если газ химически не взаимодействует с растворителем, то зависимость растворимости газа в жидкости от давления выражается законом Генри. Закон Генри справедлив только тогда, когда растворение газа в жидкости не связано с процессами диссоциации или ассоциации молекул растворенного газа. При наличии диссоциации или ассоциации молекул закон Генри следует применять отдельно к каждому роду молекул, концентрации которых не произвольны, а связаны между собой законами химического равновесия и могут быть выражены через общую концентрацию газа в растворе. В этом случае общая концентрация газа уже сложным образом связана с давлением газа над раствором. Однако в ряде случаев пропорциональность сохраняется, и тогда закон Генри остается справедливым. С изменением давления газа растворимость различных газов меняется неодинаково, и подчинение закону Генри наблюдается лишь в области невысоких давлений. Различие в растворимости определяется взаимным влиянием отдельных газов друг на друга в газовой фазе и взаимным влиянием растворенных газов в жидкой фазе. При низких давлениях, когда взаимное влияние отдельных газов невелико, закон Генри справедлив для каждого газа, входящего в газовую смесь, в отдельности.
3.1.3 Зависимость растворимости газов в жидкостях от температуры
При небольших давлениях растворимость газов в жидкостях с повышением температуры обычно уменьшается. При высоких давлениях растворимость газов в жидкостях с ростом температуры может и увеличиваться. Так, например, растворимость водорода, гелия, неона и других газов в органических растворителях и водорода в жидком аммиаке увеличивается при повышении температуры. В ряде случаев растворимость газов в жидкостях с ростом температуры проходит через минимум. Количественную зависимость растворимости газов в жидкости от температуры можно найти из условий равновесия между раствором, содержащим растворенный газ, и газовой фазой, которая при малой летучести растворителя представляет собой чистый растворяемый газ. Эта зависимость выражается уравнением:
![]() (8)
(8)
где ![]() — изменение
энтальпии в процессе перехода 1 моль газа из газообразного состояния в
состояние насыщенного раствора или последняя теплота растворения. При низких
температурах
— изменение
энтальпии в процессе перехода 1 моль газа из газообразного состояния в
состояние насыщенного раствора или последняя теплота растворения. При низких
температурах ![]() т.е. растворимость газов в жидкостях уменьшается с ростом температуры. В области
высоких температур
т.е. растворимость газов в жидкостях уменьшается с ростом температуры. В области
высоких температур ![]() т.е. растворимость газов в
жидкостях увеличивается с ростом температуры.
При температуре, которой соответствует
т.е. растворимость газов в
жидкостях увеличивается с ростом температуры.
При температуре, которой соответствует ![]() = 0, растворимость газа в
жидкости будет минимальной. В небольшом температурном интервале последняя
теплота растворения
= 0, растворимость газа в
жидкости будет минимальной. В небольшом температурном интервале последняя
теплота растворения ![]() практически постоянна. Тогда в соответствии
с уравнением (8) логарифм растворимости газа в жидкости линейно зависит от 1/Т:
практически постоянна. Тогда в соответствии
с уравнением (8) логарифм растворимости газа в жидкости линейно зависит от 1/Т:

3.2 Равновесие жидкость—жидкость в двухкомпонентных системах
Растворы жидкостей в жидкостях очень разнообразны по твоей природе и свойствам. Растворимость жидкостей в жидкостях зависит от природы растворителя и растворенного вещества, температуры, присутствия в растворе посторонних веществ. Существуют растворы с неограниченной взаимной растворимостью, ограниченной взаимной растворимостью и с практически полной взаимной нерастворимостью жидкостей. Ограниченная взаимная растворимость двух жидкостей наблюдается в системах со значительным отклонением от идеальности. Растворимость таких жидкостей зависит от температуры. В одних системах взаимная растворимость жидкостей с ростом температуры увеличивается (системы с верхней критической температурой растворения), в других уменьшается (системы с нижней критической температурой растворения). Под критической температурой растворения понимают ту температуру, при которой составы двух равновесных жидких фаз одинаковы. Для изображения зависимости взаимной растворимости жидкостей от температуры при постоянном давлении строят диаграммы состояния в координатах температура—состав (диаграммы растворимости). При критической температуре растворения оба жидких раствора по составу тождественны, и является условно инвариантной (Сусл = 2 — 2 = 0). К системам с верхней критической температурой растворения относятся системы: вода—анилин, вода—фенол, вода—нитробензол. Иногда взаимная растворимость жидкостей увеличивается как с повышением, так и с понижением температуры (системы с верхней и нижней критическими температурами растворения). В некоторых системах критические температуры растворения не достигаются, так как при повышении температуры одна из жидкостей превращается в пар, а при понижении температуры одна из жидкостей кристаллизуется.
3.3 Равновесие пар—жидкий раствор в двухкомпонентных системах
3.3.1 Равновесие пар—жидкий раствор в системах с неограниченной взаимной растворимостью жидкостей
Если раствор образован из двух летучих, неограниченно растворимых друг в друге жидкостей, то пар, находящийся в равновесии с жидким раствором, будет содержать оба компонента. В общем случае состав пара отличается от состава жидкого раствора, из которого он получен. При невысоких давлениях пар можно рассматривать как смесь идеальных газов. Если пар подчиняется законам идеальных газов и находится в равновесии с идеальным раствором, то состав паровой фазы легко найти, зная состав жидкой фазы. Согласно закону Дальтона общее давление пара над идеальным раствором равно сумме парциальных давлений пара компонентов:
![]() (9)
(9)
Во всем интервале концентраций идеального жидкого раствора растворитель и растворенное вещество подчиняются закону Рауля:
![]() (10)
(10)
Для бинарного раствора, исходя из (9) и (10),
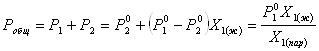 (11)
(11)
отсюда после некоторых преобразований имеем
![]()
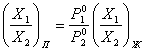 (12)
(12)
Из уравнения
(12) следует, что только при равенстве давлений пара над чистыми компонентами ![]() ) состав пара одинаков
с составом жидкого раствора, из которого он получен. Во всех остальных
случаях, даже для идеальных растворов, состав пара отличается от состава
исходного раствора.
) состав пара одинаков
с составом жидкого раствора, из которого он получен. Во всех остальных
случаях, даже для идеальных растворов, состав пара отличается от состава
исходного раствора.
Среди реально существующих растворов имеется много таких систем, для которых уравнение (12) позволяет рассчитать состав пара заданном составе жидкого раствора.
На практике чаще приходится встречаться с неидеальными растворами, которые не подчиняются закону Рауля. В этих случаях состав пара определяется опытным путем. Для изучения равновесия пар— жидкий раствор применяют два типа диаграмм состояния:
диаграммы давление пара — состав (Т — const)
диаграммы температура кипения – состав (Р – const)
На практике
для изучения равновесия пар – жидкий раствор, чаще используются диаграммы
температура—состав (диаграммы кипения). Реальные растворы со значительным положительным
или отрицательным отклонением от идеальности способны образовывать азеотропные
смеси (азеотропы), которые на диаграммах состояния. Азеотропные смеси — это
растворы, при испарении которых получается пар того же состава, что и исходная
жидкая смесь![]() .
Азеотропные смеси—условно инвариантные системы (Сусл = 2 — 2 =
0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую
температуру кипения. При изменении внешнего давления изменяется не только
температура кипения, но и состав азеотропного раствора. Это указывает на то,
что азеотропная смесь не является химическим соединением. Как для идеальных,
так и для реальных растворов справедлив первый закон Гиббса—Коновалова: пар по
сравнению с жидким раствором, из которого он получен, при равновесии богаче тем
компонентом, прибавление которого к раствору приводит к понижению температуры
кипения раствора при заданном внешнем давлении или к повышению давления пара
над раствором. В системах с азеотропными смесями добавление к раствору более летучего
компонента не всегда приводит к повышению давления пара над раствором, т.е. к
понижению температуры кипения раствора. Для реальных растворов с азеотропными
смесями справедлив также второй закон Гиббса—Коновалова: в азеотропных смесях,
составы жидкости и пара совпадают. Азеотропные
смеси образуются не только в системах со значительными отклонениями от закона
Рауля, но и в системах с незначительными отклонениями, когда компоненты
раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара
над чистыми компонентами
.
Азеотропные смеси—условно инвариантные системы (Сусл = 2 — 2 =
0). В реальных растворах азеотропная смесь имеет самую низкую или самую высокую
температуру кипения. При изменении внешнего давления изменяется не только
температура кипения, но и состав азеотропного раствора. Это указывает на то,
что азеотропная смесь не является химическим соединением. Как для идеальных,
так и для реальных растворов справедлив первый закон Гиббса—Коновалова: пар по
сравнению с жидким раствором, из которого он получен, при равновесии богаче тем
компонентом, прибавление которого к раствору приводит к понижению температуры
кипения раствора при заданном внешнем давлении или к повышению давления пара
над раствором. В системах с азеотропными смесями добавление к раствору более летучего
компонента не всегда приводит к повышению давления пара над раствором, т.е. к
понижению температуры кипения раствора. Для реальных растворов с азеотропными
смесями справедлив также второй закон Гиббса—Коновалова: в азеотропных смесях,
составы жидкости и пара совпадают. Азеотропные
смеси образуются не только в системах со значительными отклонениями от закона
Рауля, но и в системах с незначительными отклонениями, когда компоненты
раствора имеют близкие температуры кипения, т.е. почти одинаковые давления пара
над чистыми компонентами ![]() . В этом случае на диаграмме
состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше
различие между
. В этом случае на диаграмме
состояния появляется экстремум, лежащий в средней части диаграммы. Чем больше
различие между ![]() и
и ![]() , тем больше положение
экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на
кривой давления пара в сторону более летучего компонента, при минимуме — в
сторону менее летучего компонента.
, тем больше положение
экстремума сдвинуто в сторону одного из компонентов системы: при максимуме на
кривой давления пара в сторону более летучего компонента, при минимуме — в
сторону менее летучего компонента.
3.3.2 Равновесие пар — жидкий раствор в системах с ограниченной взаимной растворимостью жидкостей
Если система образована из двух летучих ограниченно смешивающихся жидкостей, то при испарении такой системы пар будет содержать оба компонента и находиться в равновесии с каждой из жидких фаз. Согласно правилу сосуществования фаз в гетерогенной системе две фазы, порознь находящиеся в равновесии с третьей фазой, равновесны и между собой. Следовательно, оба жидких раствора равновесны не только с паром, но и между собой. При равновесии химический потенциал каждого из компонентов гетерогенной системы во всех равновесных фазах одинаков:
![]() (13)
(13)
![]() (14)
(14)
При невысоких давлениях пар можно рассматривать как смесь идеальных газов. Тогда
![]() (15)
(15)
Поскольку при
заданной температуре ![]() , то парциальное давление
пара Рi одного и того же
компонента над обеими равновесными жидкими фазами одинаково. Так как общее
давление пара над раствором равно сумме парциальных давлений компонентов, то
при равновесии над обоими жидкими слоями общее давление пара также одинаково. В
расслаивающихся равновесных системах с изменением состава системы составы
равновесных жидких фаз не изменяются.
, то парциальное давление
пара Рi одного и того же
компонента над обеими равновесными жидкими фазами одинаково. Так как общее
давление пара над раствором равно сумме парциальных давлений компонентов, то
при равновесии над обоими жидкими слоями общее давление пара также одинаково. В
расслаивающихся равновесных системах с изменением состава системы составы
равновесных жидких фаз не изменяются.
Следовательно, при постоянной температуре с изменением состава расслаивающейся системы парциальные давления отдельных компонентов и общее давление пара сохраняются постоянными (правило Коновалова). Характер изменения общего и парциальных давлений пара от состава раствора с ограниченной растворимостью жидкостей показан на рис. ниже. Заштрихованная область на диаграмме соответствует области расслоения при температуре Т. Пунктирными линиями Аb и Ва показан характер изменения парциальных давлений компонентов в системе, подчиняющейся закону Рауля. Кривые аСDВ и АFНb изображают изменения парциальных давлений пара компонентов А и В, кривая аКLb — изменение общего давления пара в зависимости от состава жидких фаз.
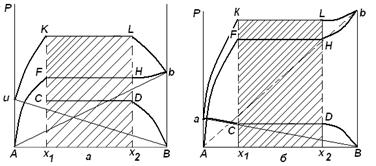
рис. зависимость общего и парциальных
давлений пара от состава раствора в системах с ограниченной взаимной растворимостью
жидкостей при Т=const. ![]()
Для изучения равновесия пар – жидкий раствор в системах с ограниченной взаимной растворимостью жидкостей, пользуются диаграммами состояния давление – состав и температура кипения – состав.
3.3.3 Равновесие пар—жидкий раствор в системах с взаимно нерастворимыми жидкостями
Совершенно
несмешивающихся жидкостей не существует, так как любые жидкости в какой-то
степени растворимы друг в друге. Однако если взаимная растворимость жидкостей
ничтожно мала, то эти жидкости можно рассматривать как взаимно нерастворимые. В
системах, состоящих из взаимно нерастворимых жидкостей, испарение каждой жидкости
происходит независимо от присутствия другой, и давление пара каждого компонента
при данной температуре сохраняется постоянным для любых соотношениях жидкостей.
Температура кипения смеси из двух взаимно
нерастворимых жидкостей ниже температур кипения чистых компонентов, так как
общее давление паров (Р) над системой выше давления пара каждого из
компонентов в отдельности (![]() и
и ![]() ) и равно
) и равно
![]() .
.
Если паровую фазу рассматривать как смесь идеальных газов, то в соответствии с законом Дальтона состав пара можно определить по уравнению
![]() ;
; ![]()
При заданной температуре пар такого состава изображается фигуративной точкой. Если составы исходной жидкой смеси и пара совпадают, то при изобарном испарении вся жидкость превращается в пар того же состава, а при конденсации такого пара образуются два жидких слоя, суммарный состав которых совпадает с составом исходной смеси. Если составы исходной смеси и пара различны, например жидкая смесь, то при давлении будут испаряться обе жидкости и образуется пар определенного состава. Дальнейшее испарение жидкого компонента приведет к изменению состава пара и к понижению давления над жидкостью. Во всем интервале давлений пар насыщен относительно одного компонента. После исчезновения жидкой фазы пар становится ненасыщенным относительно обоих компонентов и при неизменном составе будет перегреваться. При изотермическом сжатии пара рассмотренные стадии будут происходить в обратной последовательности. Таким образом, испарение и конденсация аналогичных смесей характеризуются наличием некоторого интервала давлений, в котором сосуществуют чистый жидкий компонент и паровая смесь.
4. Уравнение Клапейрона
Термодинамическое обоснование эмпирических соотношений между давлением равновесного пара и температуре было дано Клапейроном в 1834 г. Рассмотрим жидкость, находящуюся в равновесии с ее паром при температуре Т и давлении, равном давлении равновесного пара Р при этой температуре.
Термодинамическим критерием равновесия при постоянных температуре и давлении является равенство изобарных потенциалов для этих двух состояний:
![]() , (16)
, (16)
где «ж» и «пар» — индексы, обозначающие жидкость и пар.
Если температура повысилась до Т+dТ, то для того чтобы обе фазы остались в равновесии, давление должно увеличиться до Р+dР, равного давлению пара при этой более высокой температуре. При бесконечно малом повышении температуры и давления изобарный потенциал для жидкости станет равным G(ж)+dG(ж), а для пара G(пар)+dG(пар). Так как обе фазы находятся в равновесии, то
![]() (17)
(17)
С учетом уравнения (16) условие сохранения равновесия при изменении температуры и давления имеет вид:
![]() (18)
(18)
Так как dG представляет собой полный дифференциал, то уравнение (18) можно написать следующим образом:
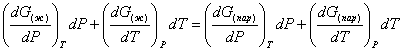 (19)
(19)
На основании
уравнений ![]() и
и
![]() уравнение
(19) можно переписать в виде
уравнение
(19) можно переписать в виде
![]() (20)
(20)
При подстановке получим
![]() (21)
(21)
Так как по уравнению
![]()
![]()
![]() (22)
(22)
где ![]() — изменение энтальпии
при испарении жидкости при температуре Т, то уравнение (21) можно написать
следующим образом:
— изменение энтальпии
при испарении жидкости при температуре Т, то уравнение (21) можно написать
следующим образом:
![]() (23)
(23)
Это важное
соотношение известно как уравнение Клапейрона. Оно дает зависимость
скорости изменения давления равновесного пара с температурой (dР/dТ) от энтальпии испарения ![]() , объема
жидкости V (ж) и объема пара V(пар) при температуре Т
и давлении, равном давлению насыщенного пара. Вследствие того что вывод
уравнения (23) не зависит от каких-либо предположений относительно природы
обеих фаз, можно легко вывести такие же уравнения для равновесия между твердым
веществом и паром, находящимся в равновесии с ним, а также для равновесия между
твердым веществом и жидкостью и между двумя различными кристаллическими формами
твердого вещества. Для этих случаев уравнение (23) можно написать так:
, объема
жидкости V (ж) и объема пара V(пар) при температуре Т
и давлении, равном давлению насыщенного пара. Вследствие того что вывод
уравнения (23) не зависит от каких-либо предположений относительно природы
обеих фаз, можно легко вывести такие же уравнения для равновесия между твердым
веществом и паром, находящимся в равновесии с ним, а также для равновесия между
твердым веществом и жидкостью и между двумя различными кристаллическими формами
твердого вещества. Для этих случаев уравнение (23) можно написать так:
![]() (24)
(24)
![]()
![]() (25)
(25)
 (26)
(26)
где ![]() ,
, ![]() и
и ![]() — энтальпии возгонки,
плавления и перехода (между твердым состоянием 1 и 2) соответственно. Теплоты
возгонки, плавления и испарения при заданной температуре связаны соотношением
— энтальпии возгонки,
плавления и перехода (между твердым состоянием 1 и 2) соответственно. Теплоты
возгонки, плавления и испарения при заданной температуре связаны соотношением
![]() (27)
(27)
поскольку количество тепла, необходимое для испарения данного количества твердого вещества, остается постоянным, независимо от того, проводится ли процесс испарения твердого вещества непосредственно или путем первоначального плавления твердого вещества с последующим испарением жидкости. Каждое из этих уравнений можно выразить через мольные величины.
При пользовании уравнениями (23) — (26) необходимо выражать изменение энтальпии процесса в тех же единицах, что и произведение давления на изменение объема. Для этой цели полезно рассчитать множитель для перевода кал в л • атм:
![]()
5. Уравнение Клаузиуса — Клапейрона
Клаузиус
показал, как можно упростить уравнение Клапейрона для случаев испарения и
возгонки, исходя из предположения, что пар подчиняется закону идеального газа и
что мольным объемом жидкости ![]() (ж) по сравнению с мольным объемом
пара
(ж) по сравнению с мольным объемом
пара ![]() (пар)
можно пренебречь. Например, для воды при 100° V(пар) =30.2 л а V(ж)=0,0188 л. Подставляя
RT/Р вместо V (пар), получим
(пар)
можно пренебречь. Например, для воды при 100° V(пар) =30.2 л а V(ж)=0,0188 л. Подставляя
RT/Р вместо V (пар), получим
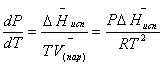 (28)
(28)
После преобразования выражение принимает вид:
![]() (29)
(29)
![]() (30)
(30)
Интегрирование в
предположении, что ![]() не зависит от температуры, дает:
не зависит от температуры, дает:
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
где С — константа интегрирования.
Теперь очевидна
теоретическая основа эмпирического соотношения ![]() . Уравнение (32) представляет
собой уравнение прямой линии, если рассматривать lnР как функцию
. Уравнение (32) представляет
собой уравнение прямой линии, если рассматривать lnР как функцию ![]() . Тангенс угла
наклона прямой равен
. Тангенс угла
наклона прямой равен ![]() а при использовании десятичных
логарифмов он равен
а при использовании десятичных
логарифмов он равен ![]() . Таким образом, теплоту испарения
можно рассчитать с применением выражения
. Таким образом, теплоту испарения
можно рассчитать с применением выражения
![]()
![]()
![]()
![]() (34)
(34)
Часто удобнее пользоваться уравнением, полученным при интегрировании в пределах Р2, Т2 и Р1, Т1:
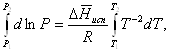 (35)
(35)
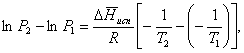 (36)
(36)
![]() (37)
(37)
По этому
уравнению можно рассчитать теплоту испарения, исходя из давления равновесного
пара при двух различных температурах; если известны теплота испарения и
давление пара при одной температуре, можно рассчитать давление пара при другой
температуре при условии, что ![]() остается постоянной. Давление
можно выразить в любых единицах, но эти единицы должны быть одинаковыми для
обоих давлений. Точно так же можно выбрать любые единицы энергии при условии,
что
остается постоянной. Давление
можно выразить в любых единицах, но эти единицы должны быть одинаковыми для
обоих давлений. Точно так же можно выбрать любые единицы энергии при условии,
что![]() и
R будут выражены в одинаковых единицах. Изменение
давления пара твердого вещества с температурой можно выразить с помощью
уравнения (37) при условии, что температурный интервал не слишком широк.
Вследствие того, что теплота возгонки твердого вещества больше, чем теплота
испарения соответствующей жидкости, давление пара твердого вещества быстрее
изменяется с температурой, чем давление пара соответствующей жидкости, и кривая
идет круче. Дифференциальное выражение (28) можно применять, если изменения
температуры и давления малы. Например, удобно пользоваться следующей формулой
для внесения поправок в температуру кипения при колебаниях атмосферного
давления:
и
R будут выражены в одинаковых единицах. Изменение
давления пара твердого вещества с температурой можно выразить с помощью
уравнения (37) при условии, что температурный интервал не слишком широк.
Вследствие того, что теплота возгонки твердого вещества больше, чем теплота
испарения соответствующей жидкости, давление пара твердого вещества быстрее
изменяется с температурой, чем давление пара соответствующей жидкости, и кривая
идет круче. Дифференциальное выражение (28) можно применять, если изменения
температуры и давления малы. Например, удобно пользоваться следующей формулой
для внесения поправок в температуру кипения при колебаниях атмосферного
давления:
![]() (38)
(38)
Так как
уравнение (37) для расчета теплоты испарения выведено в предположении, что пар
есть идеальный газ, то результаты, получаемые при пользовании этим уравнением,
не более точны, чем расчеты, в которые входит уравнение ![]() .
.
Другое
приближение содержит допущение о том, что теплота испарения не зависит от
температуры. Однако в широком интервале температур графики зависимости lgP от 1/Т несколько
искривлены, потому что ![]() меняется с температурой. В этом случае можно рассчитать
теплоту испарения для какой-нибудь определенной температуры из наклона кривой
путем проведения касательной к этой кривой при заданной температуре. Уравнение
для давления равновесного пара, которое дает линейное изменение
меняется с температурой. В этом случае можно рассчитать
теплоту испарения для какой-нибудь определенной температуры из наклона кривой
путем проведения касательной к этой кривой при заданной температуре. Уравнение
для давления равновесного пара, которое дает линейное изменение ![]() с температурой, можно вывести следующим образом. Согласно
уравнению
с температурой, можно вывести следующим образом. Согласно
уравнению ![]() зависимость
мольной теплоты испарения
зависимость
мольной теплоты испарения ![]() от
температуры выражается уравнением
от
температуры выражается уравнением
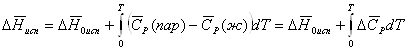 (39)
(39)
где ![]() - гипотетическая
теплота испарения при абсолютном нуле. В предположении, что
- гипотетическая
теплота испарения при абсолютном нуле. В предположении, что ![]() не зависит от
температуры,
не зависит от
температуры,
![]()
Так как
разность ![]() отрицательна,
отрицательна,
![]() уменьшается по мере повышения температуры. Именно этого
можно было ожидать на основании молекулярно-кинетических представлений, потому
что жидкость с повышением температуры расширяется, вследствие этого расстояние
между молекулами увеличивается и для их отрыва при образовании пара требуется
меньше энергии.
уменьшается по мере повышения температуры. Именно этого
можно было ожидать на основании молекулярно-кинетических представлений, потому
что жидкость с повышением температуры расширяется, вследствие этого расстояние
между молекулами увеличивается и для их отрыва при образовании пара требуется
меньше энергии.
Подставляя ![]() в
уравнение (30), получим
в
уравнение (30), получим
![]()
![]() (40)
(40)
Тогда неопределенный интеграл этого выражения равен:
![]() (41)
(41)
![]() (42)
(42)
Для определения трех констант А,В,С нужно решить систему из трех уравнений, при составлении которой необходимы точные данные при трех температурах. Уравнение (42) применимо в более широком интервале температур, чем уравнение (32), однако и оно не является точным, поскольку отклонение свойств пара от свойств идеального газа приводит к заметной ошибке, которая не учитывается при выводе уравнения.
6. Практическая часть
6.1 Вопросы
Каким правилом выражается связь между числом степеней свободы, числом фаз и числом компонентов в гетерогенной системе?
Дать понятия: гетерогенная система, фаза, составляющее вещество системы.
С помощью какого уравнения выражается связь между основными термодинамическими параметрами однокомпонентной двухфазной системы, находящейся в состоянии равновесия? Вывести это уравнение.
Свяжите составы жидкости и ее пара с общим давлением и парциальным давлением пара.
Интерпретируйте диаграмму температура – состав и используйте для ее определения поведение смеси при дистилляции.
Справедливо ли уравнение Клапейрона – Клаузиуса для фазовых переходов между твердым и газообразным агрегатными состояниями вещества? Аргументируйте свой ответ.
Что характеризует число степеней свободы равновесной термодинамической системы?
Сформулируйте основной закон фазового равновесия. Как классифицируются системы?
Охарактеризуйте однокомпонентные гетерогенные системы. Диаграмма состояния воды. Кстати, что такое фазовая диаграмма?
Что такое моно- и энантиотропные фазовые переходы? Охарактеризовать каждый из них.
6.2 Задачи
Температура кипения ртути
под нормальным атмосферным давлением 357![]() . Теплота парообразования 283,2
Дж/г. Определить изменение упругости пара ртути при изменении температуры на 1
. Теплота парообразования 283,2
Дж/г. Определить изменение упругости пара ртути при изменении температуры на 1![]() вблизи температуры
кипения ртути под нормальным атмосферным давлением.
вблизи температуры
кипения ртути под нормальным атмосферным давлением.
Решение: используем формулу ![]() откуда
откуда
![]() ,
,
где ![]() - мольная теплота
испарения. Находим
- мольная теплота
испарения. Находим
![]() ; Т=630К
; Т=630К ![]() .
.
Давление паров воды при
97![]() равно
90919,9
равно
90919,9 ![]() ,
а при 103
,
а при 103![]() 112651,8
112651,8![]() .
Определить давление паров воды при 110
.
Определить давление паров воды при 110![]() (Р110).
(Р110).
Решение: Из формулы
![]() ,
,
где ![]() - упругости паров, рассчитаем
- упругости паров, рассчитаем
![]() .
.
![]()
![]()
![]()
Определим ![]() , используя
полученное значение
, используя
полученное значение ![]() и
и ![]() при
при ![]() (К).
(К).
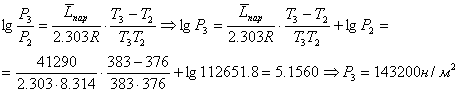
Сравним с табличной
величиной ![]() .
.
3. Удельная теплота плавления нафталина
при его нормальной температуре плавления 79,9![]() равна 149,25 Дж/г. Разность удельных
объемов в жидком и твердом состояниях при температуре плавления
равна 149,25 Дж/г. Разность удельных
объемов в жидком и твердом состояниях при температуре плавления ![]() 0,146
0,146![]() . Определить изменение
температуры плавления нафталина при увеличении давления в 100 раз по сравнению
с нормальным атмосферным давлением (101,325
. Определить изменение
температуры плавления нафталина при увеличении давления в 100 раз по сравнению
с нормальным атмосферным давлением (101,325![]() ).
).
Решение: Используя уравнение ![]() , т.к. давление дано в
, т.к. давление дано в ![]() , то изменение
удельного объема нужно выразить в
, то изменение
удельного объема нужно выразить в ![]() , а теплоту плавления в
Дж/кг. Поскольку
, а теплоту плавления в
Дж/кг. Поскольку ![]() - разность удельных объемов,
то вместо мольной теплоты плавления можно взять удельную теплоту плавления
(Дж/кг).
- разность удельных объемов,
то вместо мольной теплоты плавления можно взять удельную теплоту плавления
(Дж/кг).
![]()
Изменение температуры
плавления ![]() при
увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением
(т.е. при 1,013
при
увеличении давления в 100 раз по сравнению с нормальным атмосферным давлением
(т.е. при 1,013![]()
![]() )=3,453
)=3,453![]()
![]() =3,5
=3,5![]() .
.
4. Докажите, что на диаграмме “давление – температура” линии равновесия жидкость – пар в однокомпонентной системе всегда должна иметь положительный наклон.
Решение:
![]()
![]() и
и ![]() , поэтому
, поэтому
![]()
5. Как изменится точка кипения воды (100![]() ) при изменении атмосферного
давления на 1 мм рт.ст.? При 100
) при изменении атмосферного
давления на 1 мм рт.ст.? При 100![]() и 1 атм. теплота испарения воды 539,7
и 1 атм. теплота испарения воды 539,7
![]() , мольный
объем жидкой воды 18,78 мл, мольный объем пара 30,19 литров.
, мольный
объем жидкой воды 18,78 мл, мольный объем пара 30,19 литров.
Решение:

Отсюда![]() .
.
6. Плотность твердого фенола 1072 ![]() , жидкого 1056
, жидкого 1056 ![]() , теплота его плавления
1,044
, теплота его плавления
1,044![]() Дж/кг, температура замерзания 314,2 К. Вычислите dP/dT и температуру
плавления фенола при 5,065
Дж/кг, температура замерзания 314,2 К. Вычислите dP/dT и температуру
плавления фенола при 5,065 ![]() Па.
Па.
Решение: по уравнению Клапейрона – Клаузиуса рассчитываем dP/dT:

Чтобы вычислить температуру
плавления при заданном внешнем давлении, принимаем, что dT/dP в интервале давлений 1,0132![]() -5,065
-5,065![]() Па – величина
постоянная, равная 4,214
Па – величина
постоянная, равная 4,214![]() К/Па. Тогда
К/Па. Тогда
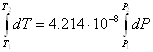 и
и ![]() .
.
7. Для каждой из следующих систем установить число компонентов
а) ![]()
б) ![]() где парциальное давление
NH3 не обязательно равно парциальному
давлению HCl.
где парциальное давление
NH3 не обязательно равно парциальному
давлению HCl.
в) ![]()
г) ![]() где СаО и СО2 образуется
при распаде СаСО3 (крист).
где СаО и СО2 образуется
при распаде СаСО3 (крист).
Решение:
а) 
б) 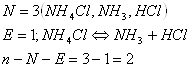
в) 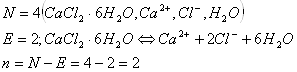
г) 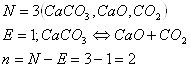
То, что СаО и СО2 присутствуют в стехиометрически равных Количествах, в данном случае не учитывается, т.к. это не влияет на состав фазы. Независимо от соотношения СаО и СО2 состав газообразной фазы всегда 100% СО2 , а состав тв. фазы всегда 100% СаО.
8. Данные по давлению паров чистых хлорбензола и воды даны в таблице.
|
t, |
p |
p |
| 50 | 93 | 42 |
| 60 | 149 | 66 |
| 70 | 234 | 98 |
| 80 | 355 | 145 |
| 90 | 526 | 208 |
| 100 | 760 | 293 |
| 110 | 1075 | 403 |
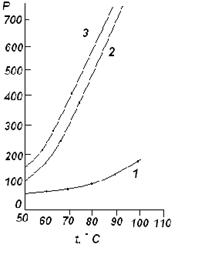
а) Приняв, что хлорбензол и вода в жидком состоянии полностью не смешиваются друг с другом, определить температуру, при которой хлорбензол будет перегоняться с паром при общем давлении 1 атм.
б) Каково будет содержание (вес. %) хлорбензола в дистиллате?
Решение: а) Построим график зависимости ![]() от t (кривая 1) и график зависимости
от t (кривая 1) и график зависимости ![]() от t (кривая 2). Исходя из этого графика,
для нескольких температур откладываем
от t (кривая 2). Исходя из этого графика,
для нескольких температур откладываем ![]() и
и ![]() , и строим зависимость (
, и строим зависимость (![]() +
+![]() ) от t (кривая 3). Кривая 3 описывает зависимость
общего давления пара системы С6Н5Сl - H2O от температуры. Температурой кипения
системы С6Н5Сl - H2O будет температура, при которой
) от t (кривая 3). Кривая 3 описывает зависимость
общего давления пара системы С6Н5Сl - H2O от температуры. Температурой кипения
системы С6Н5Сl - H2O будет температура, при которой ![]() +
+![]() =760 мм рт. ст. Как
видно из графика (кривая 3), это условие выполняется при t=91,2
=760 мм рт. ст. Как
видно из графика (кривая 3), это условие выполняется при t=91,2 ![]() .
.
б) ![]() ; А= С6Н5Сl, В= H2O. Температура кипения 92,1
; А= С6Н5Сl, В= H2O. Температура кипения 92,1![]()
![]() мм рт. ст.;
мм рт. ст.; ![]() мм рт. ст.;
МА=113; МВ=18,0;
мм рт. ст.;
МА=113; МВ=18,0;
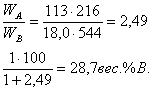
9. Используя приведенные ниже данные, постройте диаграмму для системы хлористый натрий (S) – вода (W). Примите, что твердые растворы не образуются. Обозначьте все области.
|
Температура замерзания, |
Состав насыщенного раствора, вес. % NaCl | Твердая фаза |
| 0 | 0 | W |
| -0,4 | 0,69 | W |
| -0,8 | 1,35 | W |
| -2,86 | 4,7 | W |
| -3,42 | 5,53 | W |
| -6,6 | 9,90 | W |
| -9,25 | 13,0 | W |
| -12,7 | 16,7 | W |
| -16,66 | 20,0 | W |
| -21,12(эвтектика) | 23,1 |
|
| -14 | 24,6 |
|
| +0,1(перитектика) | 26,3 |
|
| 10,0 | 26,34 | S |
| 15,0 | 26,34 | S |
| 20,0 | 26,40 | S |
| 30,0 | 26,52 | S |
| 40,0 | 26,67 | S |
| 60,0 | 27,07 | S |
| 80,0 | 27,55 | S |
| 100,0 | 28,15 | S |
Решение: Построим диаграмму
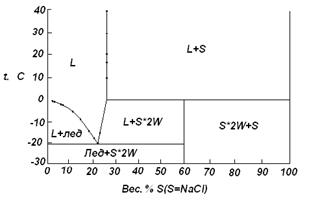
10. Докажите, что для системы, изображенной на рисунке, при равновесии
![]()
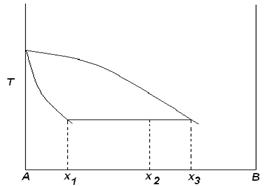
W1 – вес фазы 1, W2 – вес фазы 2, х1 –вес. % В в фазе 1, х2 – вес. % В в фазе 2; хТ – вес. % В во всей системе.
Решение: Пусть WТ – общий вес всей системы. Тогда

![]() .
.
Заключение
В введении основное
внимание уделялось основным определениям фазового равновесия. Далее в работе
были рассмотрены правило фаз Гиббса, равновесные состояния при фазовых переходах.
К ним относятся: равновесие газ – жидкий раствор в двухкомпонентных системах; равновесие жидкость—жидкость в двухкомпонентных системах;
равновесие пар—жидкий раствор в двухкомпонентных системах с
ограниченной и неограниченной взаимной растворимостью жидкостей; равновесие
пар—жидкий раствор в системах с взаимно нерастворимыми жидкостями. Также было
рассмотрено Уравнение Клаузиуса — Клапейрона, в котором Клаузиус показал, как можно упростить уравнение Клапейрона
для случаев испарения и возгонки, исходя из предположения, что пар подчиняется
закону идеального газа и что мольным объемом жидкости ![]() (ж) по сравнению с мольным объемом
пара
(ж) по сравнению с мольным объемом
пара ![]() (пар)
можно пренебречь. В практической части к данной теме были задано ряд вопросов и
10 задач с решениями.
(пар)
можно пренебречь. В практической части к данной теме были задано ряд вопросов и
10 задач с решениями.
Библиографический список
1. Даниэльс «Физическая химия», Фаррингтон, Олберти; 1978г
2. К. С. Краснов «Физическая химия» том I, Москва «Высшая школа» 2001г
3. Д. Г. Кнорре «Физическая химия», Л. Ф. Крылова, В. С. Музыкантов; Москва «Высшая школа» 1990 г
4. http://ru.wikipedia.org.
5. Лабовиц «Задачи по физической химии с решениями», Аренс; 1972 г
6. Захарченко «Сборник задач и упражнений по физической и коллоидной химии» 1978 г
7. И. И. Климов «Сборник вопроов и задач по физической и коллоидной химии», А. И Филько; 1975 г
Перепечатка материалов без ссылки на наш сайт запрещена