Контрольная работа: Статистические задачи

Контрольная работа: Статистические задачи

ЗАДАЧА 1

По исходным данным вычислить основные аналитические показатели рядов динамики (по цепной и базисной схемам):

а)  средний уровень ряда динамики;

б)  абсолютный прирост;

в)  темп роста;

г)  темп прироста;

д)  абсолютное значение 1% прироста;

е)  средний темп роста и средний темп прироста.

Средний уровень интервального ряда определим по формуле:

где Yi – значение грузооборота;

n – число значений в динамическом ряду.

Абсолютный прирост относительно базисного уровня грузооборота определим по формуле:

ΔYi=Yi-Y0

Абсолютный прирост грузооборота относительно предшествующего года определим по формуле:

ΔYi=Yi-Yi-1

Темп роста относительно базисного уровня грузооборота определим по формуле:

Темп роста грузооборота относительно предшествующего года определим по формуле:

Темп прироста относительно базисного уровня грузооборота определим по формуле:

Темп прироста грузооборота относительно предшествующего года определим по формуле:

Средний темп роста грузооборота определим по формуле:

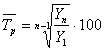
Средний темп прироста грузооборота определим по формуле:

Абсолютное значение одного процента прироста определим по формуле:

Результаты расчёта аналитических показателей ряда динамики представим в таблице 1.1

Таблица 1 – Основные аналитические показатели ряда динамики

Показатель	Схема счета	Периоды
		1	2	3	4	5	6	7	8
Уровень ряда		1199	1253	1573	1385	1276	1385	1266	1358
Средний уровень ряда		1336,875
Абсолютный прирост	Базисная	100	54,0	374,0	186,0	77,0	186	67	159
	Цепная	100	54,0	320,0	-188,0	-109,0	109,0	-119,0	92,0
Темп роста	Базисная	100	104,5	131,2	115,5	106,4	115,5	105,6	113,3
	Цепная	100	104,5	125,5	88,0	92,1	108,5	91,4	107,3
Темп прироста	Базисная	100	4,5	31,2	15,5	6,4	15,5	5,6	13,3
	Цепная	100	4,5	25,5	-12,0	-7,9	8,5	-8,6	7,3
Абсолютное значение 1% прироста			11,99	12,53	15,73	13,85	12,76	13,85	12,66
Средний темп роста		101,79
Средний темп прироста		1,79

Произведем сглаживание данных за три года при помощи двенадцатимесячной скользящей средней, централизованной на седьмой месяц. Рассчитаем коэффициент сезонности по данным трех лет, и построим график сезонной волны.

Сглаживание рядов динамики производится с помощью простых средних, скользящей средней, методами аналитического выравнивания. Скользящие средние рассчитываются по формулам:

;

 и т.д. - нецентрализованная

 - централизованная

Коэффициент сезонности определяется как отношение уровней ряда к их среднему уровню по формуле:

Средний коэффициент сезонности за рассматриваемый период находим по формуле:

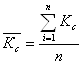
где n – количество рассчитанных коэффициентов сезонности по одноименным месяцам.

Расчет скользящей средней и коэффициента сезонности приведем в таблице 1.2.

Простроим график сезонной волны по средним коэффициентам сезонности. График приведен на рисунке 1.

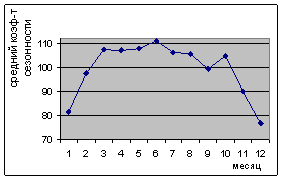
Рисунок 1 – График сезонной волны

Таблица 2 – Расчет коэффициента сезонности

Год	Месяц	Уровень ряда	Скользящая средняя		Коэффициент сезонности	Средний коэффициент сезонности
			нецентрированная	центрированная
1994	1	21,1
	2	22,8
	3	23,9
	4	23,8
	5	24,5
	6	24,6	23,550
	7	25,9	23,492	23,521	104,016
	8	25,7	23,617	23,554	103,213
	9	24,2	23,783	23,700	97,189
	10	25,5	23,942	23,863	102,410
	11	22,3	24,067	24,004	89,558
	12	18,3	24,217	24,142	73,494
1995	1	20,4	24,308	24,263	81,928	81,53
	2	24,3	24,408	24,358	97,590	97,39
	3	25,9	24,500	24,454	104,016	107,23
	4	25,7	24,592	24,546	103,213	107,03
	5	26	24,608	24,600	104,418	107,83
	6	26,4	24,750	24,679	106,024	110,84
	7	27	24,733	24,742	108,434	106,22
	8	26,9	24,725	24,729	108,032	105,62
	9	25,3	24,858	24,792	101,606	99,40
	10	26,6	25,017	24,938	106,827	104,62
	11	22,5	25,158	25,088	90,361	89,96
	12	20	25,358	25,258	80,321	76,91
1996	1	20,2	25,517	25,438	81,124
	2	24,2	25,942	25,729	97,189
	3	27,5	26,325	26,133	110,442
	4	27,6	26,367	26,346	110,843
	5	27,7	26,467	26,417	111,245
	6	28,8	26,400	26,433	115,663
	7	28,9
	8	32
	9	29,9
	10	27,1
	11	23,7
	12	19,2
Итого:		896,4
Средняя:		24,90

Из графика видно, что коэффициент сезонности в начале года увеличивается, а в конце - уменьшается. Наибольшее отклонение наблюдается в начале года 2-ой и 10 -ой месяц.

ЗАДАЧА 2

Произвести аналитическое выравнивание рядов динамики по данным задачи 1 о размерах грузооборота по родам грузов:

а)  при равномерном развитии y = a0 + a1t ;

б)  при развитии с переменным ускорением (замедлением) yt = a0 + a1t + a2t2 + a3t3 ;

в)  при изучении сезонных колебаний по данным об отправлении грузов yt = a0 + (ak cosRt + bk sinRt) .

Результаты расчётов представить в виде таблиц и графиков.

1. Способ отсчета времени от условного начала, когда ∑t=0, дает возможность определить параметры математической функции по формулам:

 

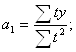
Результаты вычислений приведем в таблице 3:

Таблица 3 – Вычисление параметров функции y=a0+a1t и y=a0+a1t+a2t2+a3t3

Год	t	y	t²	ty	t4	t6	t²y	t³y	Yti*	Yt	(Yti*-y)²	(Yt-y)²
1	-4	1199	16	256	4096	-4796	19184	-76736	1324,2	1175,2	15677,13	566,75
2	-3	1253	9	81	729	-3759	11277	-33831	1327,4	1354,3	5531,64	10254,93
3	-2	1573	4	16	64	-3146	6292	-12584	1330,5	1432,5	58786,04	19730,33
4	-1	1385	1	1	1	-1385	1385	-1385	1333,7	1438,1	2630,84	2817,52
5	1	1276	1	1	1	1276	1276	1276	1340,0	1343,3	4101,34	4532,35
6	2	1385	4	16	64	2770	5540	11080	1343,2	1299,2	1746,54	7364,77
7	3	1266	9	81	729	3798	11394	34182	1346,4	1294,6	6460,14	820,27
8	4	1358	16	256	4096	5432	21728	86912	1349,5	1357,8	71,54	0,05
итого	0	10695	60	708	9780	190	78076	8914	10695,0	10695,0	95005,21	46086,98

Тогда:

 

Уравнение при равномерном развитии:

y = 1336,88 - 3,17 ∙ t

2. Для вычисления параметров функции y=a0+a1t+a2t2+a3t3 :

 

 

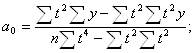
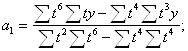
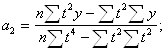
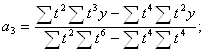
Тогда:

 

 

Уравнение при развитии с переменным ускорением (замедлением):

yt= 1398,98 - 52,06 t - 8,28 t2 + 4,68 t3;

3. По рассмотренным моделям определим теоретические уровни тренда. Фактические и теоретические уровни ряда нанесём на график, представленный на рисунке 2.

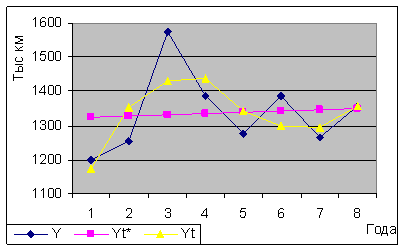
Рисунок 2 – График фактических и теоретических уровней ряда

Рассчитаем стандартизированную ошибку аппроксимации –

  

4. При изучении сезонных колебаний по данным об отправлении грузов  необходимо рассчитать параметры:

  

Результаты расчётов сведём в таблицу 4

Таблица 4 – Выравнивание ряда динамики y=a0+(aкcosRt+ bкsinRt), 1998 год

Месяц	ti	yi	cos ti	sin ti	yi∙cos ti	yi∙sin ti	yti
1	0	21,10	1	0	21,1	0	21,21
2	(1:6)π	22,80	0,86616	0,5	19,748	11,4	21,66
3	(1:3) π	23,90	0,5	0,866	11,95	20,6974	22,62
4	(1:2) π	23,80	0	1	0	23,8	23,82
5	(2:3) π	24,50	-0,5	0,866	-12,25	21,217	24,96
6	(5:6) π	24,60	-0,866	0,5	-21,3	12,3	25,71
7	π	25,90	-1	0	-25,9	0	25,89
8	(7:6) π	25,70	-0,866	-0,5	-22,26	-12,85	25,44
9	(4:3) π	24,20	-0,5	-0,866	-12,1	-20,9572	24,48
10	(3:2) π	25,50	0	-1	0	-25,5	23,28
11	(5:3) π	22,30	0,5	-0,866	11,15	-19,3118	22,14
12	(11:6) π	18,30	0,866	-0,5	15,848	-9,15	21,39
	-	282,6			-14,01	1,6454	282,60

  

Фактические и теоретические уровни ряда нанесём на график, представленный на рисунке 3.

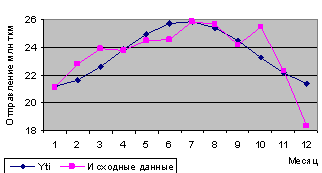
Рисунок 3 – График фактических и теоретических уровней ряда выравнивания

Фактические и теоретические уровни ряда близки по значению, а кривая ряда (рисунок 3) похожа на гармоническую функцию.

Поэтому функцию  можно использовать для выравнивания ряда динамики.

ЗАДАЧА 3

По данным таблицы определить:

1) выполнение норм удельного расхода топлива по отделениям и дороге в целом;

2) сводный индекс расхода топлива на дороге;

3) изменение среднего удельного расхода топлива на дороге за счет изменения удельного расхода топлива на 10000 т/км брутто на отделениях и за счет изменения структуры грузооборота по отделениям, а также за счет того и другого фактора одновременно;

4) абсолютный размер экономии (перерасхода) топлива за счет изменения грузооборота на отделениях, за счет изменения удельного расхода топлива на отделениях.

Таблица 10 – Грузооборот и удельный расход топлива по отделениям железной дороги

Отделение	Удельный расход топлива, кг/10000 т·км брутто.		Грузооборот брутто, млн. т·км			Выполнение норм удельного расхода топлива, %	Расход топлива, тонн
	Норма	Факти-чески	Норма	Факти-чески	% выпол-нения		План	Факт	Отчетного по удельному расходу базисного
1	50	47	200	113	56,5	94,0	10000	5311	5650
2	55	57	320	102	31,9	103,6	17600	5814	5610
3	48	45	400	101	25,3	93,8	19200	4545	4848
			920	316	113,6		46800	15670	16108

1) выполнение норм удельного расхода топлива по отделениям и дороги в целом

Iи=∑и1q1 / ∑и0q1 =15670 / 16108 = 0,973

2) Сводный индекс расхода топлива

Iиq=∑и1q1 / ∑и0q0 =15670 / 46800 = 0,335

3) Индекс удельного расхода топлива переменного состава

Iи = ∑и1q1/∑q1 : ∑и0q0/∑q0 = ∑и1q1/∑и0q1= 15670/316 : 46800/920 = 0,975

Индекс удельного расхода топлива постоянного состава

Iи=∑и1q1/∑q1 : ∑и0q1/∑q1= ∑и1q1/∑и0q1 = 15670 / 16108 = 0,973

Индекс структурных сдвигов

Iстр= ∑и0q1/∑q1 : ∑и0q0/∑q0 = 16108/316 : 46800/920 = 1,002

4) Экономия топлива за счет изменения удельного расхода

Δиq=∑и1q1-∑и0q1= 15670 - 16108 = -438 кг за счет изменения грузооборота

Δиqq=∑и0q1-∑и0q0= 16108 - 46800 = -30692 кг

ЗАДАЧА 4

№ 1. Для изучения производительности труда токарей на машиностроительном заводе было проведено 10%-ное выборочное обследование 100 рабочих методом случайного бесповторного отбора. В результате обследования получены данные о часовой выработке рабочих:

Часовая выработка, шт.	18-20	20-22	22-24	24-26	26-28	28-30
Число рабочих	2	8	24	50	12	4

С вероятностью 0,997 определите пределы, в которых находится среднее время обработки одной детали токарями завода.

Рассчитаем среднюю ошибку выборки по формуле:

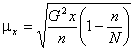
Дисперсия

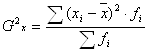
где хi - часовая выработка

 - средняя часовая выработка по всем рабочим выборки;

fi - сумма всех частот

Часовая выработка, шт.	18-20	20-22	22-24	24-26	26-28	28-30
Число рабочих	2	8	24	50	12	4	100
	40	176	576	1300	288	120	2500
(xi - )2	-10	-24	-24	50	36	20	48

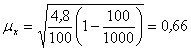
∆х = ± t · μx ∆х = ± 3 · 0,66 = 2 шт.

Ответ: с вероятностью 0,997 можно утверждать, что доля лиц, которая одобрит составит 54% - 66%.

Литература

1.  Быченко О.Г. Общая теория статистики: Задание на контрольную работу № 1 с методическими указаниями. – Гомель: БелГУТ, 2000. – 30 с.

2.  Быченко О.Г. Общая теория статистики: Задание на контрольную работу № 2 с методическими указаниями. – Гомель: БелГУТ, 2000. – 31 с.

3.  Общая теория статистики: Учебник/Т.В. Рябушкин, М.Р. Ефимова, Н.И. Яковлева. – М.: Финансы и статистика, 1981. – 279 с., ил.