Контрольная работа: Статистические способы обработки экспериментальных данных

Контрольная работа: Статистические способы обработки экспериментальных данных

Московский государственный социальный университет

Филиал в г. Минске

СТАТИСТИЧЕСКИЕ СПОСОБЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Контрольная работа по предмету

"Основы психологического экспериментирования"

студентки 5 курса з/о

Минск 2005

Содержание

Введение

1. Методы первичной статистической обработки результатов эксперимента

1.1 Мода

1.2 Медиана

1.3 Выборочное среднее

1.4 Разброс выборки

1.5 Дисперсия

2. Методы вторичной статистической обработки результатов эксперимента

2.1 Регрессионное исчисление

2.2 Корреляция

2.3 Факторный анализ

Заключение

Литература

Введение

Методы статистической обработки результатов эксперимента.

Методами статистической обработки результатов эксперимента называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами.

Некоторые из методов математико-статистического анализа позволяют вычислять так называемые элементарные математические статистики, характеризующие выборочное распределение данных, например выборочное среднее, выборочная дисперсия, мода, медиана и ряд других. Иные методы математической статистики, например дисперсионный анализ, регрессионный анализ, позволяют судить о динамике изменения отдельных статистик выборки. С помощью третьей группы методов, скажем, корреляционного анализа, факторного анализа, методов сравнения выборочных данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые исследуют в данном эксперименте.

1. Методы первичной статистической обработки результатов эксперимента

Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов психодиагностики. Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.

К первичным методам статистической обработки относят, например, определение выборочной средней величины, выборочной дисперсии, выборочной моды и выборочной медианы. В число вторичных методов обычно включают корреляционный анализ, регрессионный анализ, методы сравнения первичных статистик у двух или нескольких выборок.

Рассмотрим методы вычисления элементарных математических статистик.

1.1 Мода

Числовой характеристикой выборки, как правило, не требующей вычислений, является так называемая мода. Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке. Для симметричных распределений признаков, в том числе для нормального распределения, значение моды совпадает со значениями среднего и медианы. Для других типов распределении, несимметричных, это не характерно. К примеру, в последовательности значений признаков 1, 2, 5, 2, 4, 2, 6, 7, 2 модой является значение 2, так как оно встречается чаще других значений - четыре раза.

Моду находят согласно следующим правилам:

1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды. Например: 5, 5, 6, 6, 7, 7 - в этой выборке моды нет.

2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений. Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина =3,5

3) Если два несмежных (не соседних) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. Например, в ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной.

Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод).

4) Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой.

1.2 Медиана

Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Например, для выборки 2, 3, 4, 4, 5, 6, 8, 7, 9 медианой будет значение 5, так как слева и справа от него остается по четыре показателя. Если ряд включает в себя четное число признаков, то медианой будет среднее, взятое как полусумма величин двух центральных значений ряда. Для следующего ряда 0, 1, 1, 2, 3, 4, 5, 5, 6, 7 медиана будет равна 3,5.

Знание медианы полезно для того, чтобы установить, является ли распределение частных значений изученного признака симметричным и приближающимся к так называемому нормальному распределению. Средняя и медиана для нормального распределения обычно совпадают или очень мало отличаются друг от друга. Если выборочное распределение признаков нормально, то к нему можно применять методы вторичных статистических расчетов, основанные на нормальном распределении данных. В противном случае этого делать нельзя, так как в расчеты могут вкрасться серьезные ошибки.

1.3 Выборочное среднее

Выборочное среднее (среднее арифметическое) значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.

Выборочное среднее определяется при помощи следующей формулы:

где х - выборочная средняя величина или среднее арифметическое значение по выборке; n - количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина; хk - частные значения показателей у отдельных испытуемых. Всего таких показателей n, поэтому индекс k данной переменной принимает значения от 1 до n; ∑ - принятый в математике знак суммирования величин тех переменных, которые находятся справа от этого знака. Выражение соответственно означает сумму всех х с индексом k, от 1до n. В психодиагностике и в экспериментальных психолого-педагогических исследованиях среднее, как правило, не вычисляется с точностью, превышающей один знак после запятой, т.е. с большей, чем десятые доли единицы. В психодиагностических обследованиях большая точность расчетов не требуется и не имеет смысла, если принять во внимание приблизительность тех оценок, которые в них получаются, и достаточность таких оценок для производства сравнительно точных расчетов.

1.4 Разброс выборки

Разброс (иногда эту величину называют размахом) выборки обозначается буквой R. Это самый простой показатель, который можно получить для выборки - разность между максимальной и минимальной величинами данного конкретного вариационного ряда, т.е.

R= хmax - хmin

Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот. Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Например, даны две выборки:

Х = 10 15 20 25 30 35 40 45 50X = 30 R = 40

Y = 10 28 28 30 30 30 32 32 50 Y=30 R = 40

При равенстве средних и разбросов для этих двух выборочных рядов характер их варьирования различен. Для того чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям.

1.5 Дисперсия

Дисперсия - это среднее арифметическое квадратов отклонений значений переменной от её среднего значения.

Дисперсия как статистическая величина характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения или разброс данных.

где 5 - выборочная дисперсия, или просто дисперсия;

2 (……) - выражение, означающее, что для всех х, от первого до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;

п - количество испытуемых в выборке или первичных значений, по которым вычисляется дисперсия. Однако сама дисперсия, как характеристика отклонения от среднего, часто неудобна для интерпретации. Для того, чтобы приблизить размерность дисперсии к размерности измеряемого признака применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют стандартным отклонением.

Из суммы квадратов, делённых на число членв ряда извлекаеся квадратный корень.

Иногда исходных частных первичных данных, которые подлежат статистической обработке, бывает довольно много, и они требуют проведения огромного количества элементарных арифметических операций. Для того чтобы сократить их число и вместе с тем сохранить нужную точность расчетов, иногда прибегают к замене исходной выборки частных эмпирических данных на интервалы. Интервалом называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением.

2. Методы вторичной статистической обработки результатов эксперимента

С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, чем методы первичной статистической обработки, и требуют от исследователя хорошей подготовки в области элементарной математики и статистики. (7).

Обсуждаемую группу методов можно разделить на несколько подгрупп:

1. Регрессионное исчисление.

2. Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам.

3. Методы установления статистических взаимосвязей между переменными, например их корреляции друг с другом.

4. Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ). Рассмотрим каждую из выделенных подгрупп методов вторичной статистической обработки на примерах.

2.1 Регрессионное исчисление

Регрессионное исчисление - это метод математической статистики, позволяющий свести частные, разрозненные данные к некоторому линейному графику, приблизительно отражающему их внутреннюю взаимосвязь, и получить возможность по значению одной из переменных приблизительно оценивать вероятное значение другой переменной (7).

Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшие предсказания зависимой переменой (Y) по независимым переменным (X).

Регрессию выражают с помощью двух уравнений регрессии, которые в самом прямом случае выглядят, как уравнения прямой.

Y = a 0 + a 1 * X (1)

X = b 0 + b 1 * Y (2)

В уравнении (1) Y - зависимая переменная, X - независимая переменная, a 0 - свободный член, a 1 - коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.

В уравнении (2) X - зависимая переменная, Y - независимая переменная, b 0 - свободный член, b 1 - коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.

Количественное представление связи (зависимости) между Х и Y (между Y и X) называется регрессионным анализом. Главная задача регрессионного анализа заключается в нахождении коэффициентов a 0, b 0, a1и b 1 и определении уровня значимости полученных аналитических выражений, связывающих между собой переменные Х и У.

При этом коэффициенты регрессии a 1 и b 1 показывают, насколько в среднем величина одной переменной изменяется при изменении на единицу меры другой. Коэффициент регрессии a 1 в уравнении можно подсчитать по формуле:

а коэффициент b 1 в уравнении по формуле

где ryx - коэффициент корреляции между переменными X и Y;

Sx - среднеквадратическое отклонение, подсчитанное для переменной X;

Sy - среднеквадратическое отклонение, подсчитанное для переменной У/

Для применения метода линейного регрессионного анализа необходимо соблюдать следующие условия:

1. Сравниваемые переменные Х и Y должны быть измерены в шкале интервалов или отношений.

2. Предполагается, что переменные Х и Y имеют нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных должно быть одинаковым. (5).

2.2 Корреляция

Следующий метод вторичной статистической обработки, посредством которого выясняется связь или прямая зависимость между двумя рядами экспериментальных данных, носит название метод корреляций. Он показывает, каким образом одно явление влияет на другое или связано с ним в своей динамике. Подобного рода зависимости существуют, к примеру, между величинами, находящимися в причинно-следственных связях друг с другом. Если выясняется, что два явления статистически достоверно коррелируют друг с другом и если при этом есть уверенность в том, что одно из них может выступать в качестве причины другого явления, то отсюда определенно следует вывод о наличии между ними причинно-следственной зависимости. (7)

Когда повышение уровня одной переменной сопровождается повышением уровня другой, то речь идёт о положительной корреляции. Если же рост одной переменной происходит при снижении уровня другой, то говорят об отрицательной корреляции. При отсутствии связи переменных мы имеем дело с нулевой корреляцией. (1)

Имеется несколько разновидностей данного метода: линейный, ранговый, парный и множественный. Линейный корреляционный анализ позволяет устанавливать прямые связи между переменными величинами по их абсолютным значениям. Эти связи графически выражаются прямой линией, отсюда название "линейный". Ранговая корреляция определяет зависимость не между абсолютными значениями переменных, а между порядковыми местами, или рангами, занимаемыми ими в упорядоченном по величине ряду. Парный корреляционный анализ включает изучение корреляционных зависимостей только между парами переменных, а множественный, или многомерный, - между многими переменными одновременно. Распространенной в прикладной статистике формой многомерного корреляционного анализа является факторный анализ. (5)

Коэффициент линейной корреляции определяется при помощи следующей формулы:

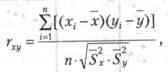
где rxy - коэффициент линейной корреляции;

х, у - средние выборочные значения сравниваемых величин;

хi, уi - частные выборочные значения сравниваемых величин;

n - общее число величин в сравниваемых рядах показателей;

S2x, S2y - дисперсии, отклонения сравниваемых величин от средних значений.

К коэффициенту ранговой корреляции в психолого-педагогических исследованиях обращаются в том случае, когда признаки, между которыми устанавливается зависимость, являются качественно различными и не могут быть достаточно точно оценены при помощи так называемой интервальной измерительной шкалы. Интервальной называют такую шкалу, которая позволяет оценивать расстояния между ее значениями и судить о том, какое из них больше и насколько больше другого. Например, линейка, с помощью которой оцениваются и сравниваются длины объектов, является интервальной шкалой, так как, пользуясь ею, мы можем утверждать, что расстояние между двумя и шестью сантиметрами в два раза больше, чем расстояние между шестью и восемью сантиметрами. Если же, пользуясь некоторым измерительным инструментом, мы можем только утверждать, что одни показатели больше других, но не в состоянии сказать на сколько, то такой измерительный инструмент называется не интервальным, а порядковым.

Большинство показателей, которые получают в психолого-педагогических исследованиях, относятся к порядковым, а не к интервальным шкалам (например, оценки типа "да", "нет", "скорее нет, чем да" и другие, которые можно переводить в баллы), поэтому коэффициент линейной корреляции к ним неприменим. В этом случае обращаются к использованию коэффициента ранговой корреляции, формула которого следующая:

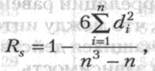
где Rs - коэффициент ранговой корреляции по Спирмену;

di - разница между рангами показателей одних и тех же испытуемых в упорядоченных рядах;

n - число испытуемых или цифровых данных (рангов) в коррелируемых рядах.

Метод множественных корреляций в отличие от метода парных корреляций позволяет выявить общую структуру корреляционных зависимостей, существующих внутри многомерного экспериментального материала, включающего более двух переменных, и представить эти корреляционные зависимости в виде некоторой системы.

Для применения частного коэффициента корреляции необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.

2. Предполагается, что все переменные имеют нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.

4. Для оценки уровня достоверности корреляционного отношения Пирсона следует пользоваться формулой (11.9) и таблицей критических значений для t-критерия Стьюдента при k = n - 2. (5)

2.3 Факторный анализ

Факторный анализ - статистический метод, который используется при обработке больших массивов экспериментальных данных. Задачами факторного анализа являются: сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных, поэтому факторный анализ используется как метод сокращения данных или как метод структурной классификации.

Важное отличие факторного анализа от всех описанных выше методов заключается в том, что его нельзя применять для обработки первичных, или, как говорят, "сырых", экспериментальных данных, т.е. полученных непосредственно при обследовании испытуемых. Материалом для факторного анализа служат корреляционные связи, а точнее - коэффициенты корреляции Пирсона, которые вычисляются между переменными (т.е. психологическими признаками), включенными в обследование. Иными словами, факторному анализу подвергают корреляционные матрицы, или, как их иначе называют, матрицы интеркорреляций. Наименования столбцов и строк в этих матрицах одинаковы, так как они представляют собой перечень переменных, включенных в анализ. По этой причине матрицы интеркорреляций всегда квадратные, т.е. число строк в них равно числу столбцов, и симметричные, т.е. на симметричных местах относительно главной диагонали стоят одни и те же коэффициенты корреляции.

Главное понятие факторного анализа - фактор. Это искусственный статистический показатель, возникающий в результате специальных преобразований таблицы коэффициентов корреляции между изучаемыми психологическими признаками, или матрицы интеркорреляций. Процедура извлечения факторов из матрицы интеркорреляций называется факторизацией матрицы. В результате факторизации из корреляционной матрицы может быть извлечено разное количество факторов вплоть до числа, равного количеству исходных переменных. Однако факторы, выделяемые в результате факторизации, как правило, неравноценны по своему значению. (5)

С помощью выявленных факторов объясняют взаимозависимость психологических явлений. (7)

Чаще всего в итоге факторного анализа определяется не один, а несколько факторов, по-разному объясняющих матрицу интеркорреляций переменных. В таком случае факторы делят на генеральные, общие и единичные. Генеральными называются факторы, все факторные нагрузки которых значительно отличаются от нуля (нуль нагрузки свидетельствует о том, что данная переменная никак не связана с остальными и не оказывает на них никакого влияния в жизни). Общие - это факторы, у которых часть факторных нагрузок отлична от нуля. Единичные - это факторы, в которых существенно отличается от нуля только одна из нагрузок. (7)

Факторный анализ может быть уместен, если выполняются следующие критерии.

1. Нельзя факторизовать качественные данные, полученные по шкале наименований, например, такие, как цвет волос (черный / каштановый / рыжий) и т.п.

2. Все переменные должны быть независимыми, а их распределение должно приближаться к нормальному.

3. Связи между переменными должны быть приблизительно линейны или, по крайней мере, не иметь явно криволинейного характера.

4. В исходной корреляционной матрице должно быть несколько корреляций по модулю выше 0,3. В противном случае достаточно трудно извлечь из матрицы какие-либо факторы.

5. Выборка испытуемых должна быть достаточно большой. Рекомендации экспертов варьируют. Наиболее жесткая точка зрения рекомендует не применять факторный анализ, если число испытуемых меньше 100, поскольку стандартные ошибки корреляции в этом случае окажутся слишком велики.

Однако если факторы хорошо определены (например, с нагрузками 0,7, а не 0,3), экспериментатору нужна меньшая выборка, чтобы выделить их. Кроме того, если известно, что полученные данные отличаются высокой надежностью (например, используются валидные тесты), то можно анализировать данные и по меньшему числу испытуемых. (5).

 

2.4 Использование факторного анализа в психологии

Факторный анализ широко используется в психологии в разных направлениях, связанных с решением как теоретических, так и практических проблем.

В теоретическом плане использование факторного анализа связано с разработкой так называемого факторно-аналитического подхода к изучению структуры личности, темперамента и способностей. Использование факторного анализа в этих сферах основано на широко принятом допущении, согласно которому наблюдаемые и доступные для прямого измерения показатели являются лишь косвенными и/или частными внешними проявлениями более общих характеристик. Эти характеристики, в отличие от первых, являются скрытыми, так называемыми латентными переменными, поскольку они представляют собой понятия или конструкты, которые не доступны для прямого измерения. Однако они могут быть установлены путем факторизации корреляционных связей между наблюдаемыми чертами и выделением факторов, которые (при условии хорошей структуры) можно интерпретировать как статистическое выражение искомой латентной переменной.

Хотя факторы имеют чисто математический характер, предполагается, что они репрезентируют скрытые переменные (теоретически постулируемые конструкты или понятия), поэтому названия факторов нередко отражают сущность изучаемого гипотетического конструкта.

В настоящее время факторный анализ широко используется в дифференциальной психологии и психодиагностике. С его помощью можно разрабатывать тесты, устанавливать структуру связей между отдельными психологическими характеристиками, измеряемыми набором тестов или заданиями теста.

Факторный анализ используется также для стандартизации тестовых методик, которая проводится на репрезентативной выборке испытуемых.

Для более подробного ознакомления с различными вариантами применения факторного анализа в психологии рекомендуем следующую литературу:

Благуш П. Факторный анализ с обобщениями. М.: Финансы и статистика, 1989.

Иберла К. Факторный анализ. М.: Статистика, 1980.

Ким Дж.О., Мьюллер Ч.У. Факторный анализ: статистические методы и практические вопросы // Факторный, дискриминационный и кластерный анализ. М.: Финансы и статистика, 1989.

Окунь Я. Факторный анализ. М.: Статистика, 1974.

Харман Г. Современный факторный анализ. М.: Статистика, 1972. (5)

Заключение

Если данные, полученные в эксперименте, качественного характера, то правильность делаемых на основе их выводов полностью зависит от интуиции, эрудиции и профессионализма исследователя, а также от логики его рассуждений. Если же эти данные количественного типа, то сначала проводят их первичную, а затем вторичную статистическую обработку. Первичная статистическая обработка заключается в определении необходимого числа элементарных математических статистик. Такая обработка почти всегда предполагает как минимум определение выборочного среднего значения. В тех случаях, когда информативным показателем для экспериментальной проверки предложенных гипотез является разброс данных относительного среднего, вычисляется дисперсия или квадратическое отклонение. Значение медианы рекомендуется вычислять тогда, когда предполагается использовать методы вторичной статистической обработки, рассчитанные на нормальное распределение, Для такого рода распределения выборочных данных медиана, а также мода совпадают или достаточно близки к средней величине. Этим критерием можно воспользоваться для того, чтобы приблизительно судить о характере полученного распределения первичных данных.

Вторичная статистическая обработка (сравнение средних, дисперсий, распределений данных, регрессионный анализ, корреляционный анализ, факторный анализ и др.) проводится в том случае, если для решения задач или доказательства предложенных гипотез необходимо определить статистические закономерности, скрытые в первичных экспериментальных данных. Приступая к вторичной статистической обработке, исследователь прежде всего должен решить, какие из различных вторичных статистик ему следует применить для обработки первичных экспериментальных данных. Решение принимается на основе учета характера проверяемой гипотезы и природы первичного материала, полученного в результате проведения эксперимента. Приведем несколько рекомендаций на этот счет.

Рекомендация 1. Если экспериментальная гипотеза содержит предположение о том, что в результате проводимого психолого-педагогического исследования возрастут (или уменьшатся) показатели какого-либо качества, то для сравнения до - и постэкспериментальных данных рекомендуется использовать критерий Стъюдента или χ2-критерий. К последнему обращаются в том случае, если первичные экспериментальные данные относительны и выражены, например, в процентах.

Рекомендация 2. Если экспериментально проверяемая гипотеза включает в себя утверждение о причинно-следственной зависимости между некоторыми переменными, то её целесообразно проверять, обращаясь к коэффициентам линейной или ранговой корреляции. Линейная корреляция используется в том случае, когда измерения независимой и зависимой переменных производятся при помощи интервальной шкалы, а изменения этих переменных до и после эксперимента небольшие. К ранговой корреляции обращаются тогда, когда достаточно оценить изменения, касающиеся порядка следования друг за другом по величине независимых и зависимых переменных, или когда их изменения достаточно велики, или когда измерительный инструмент был порядковым, а не интервальным.

Рекомендация 3. Иногда гипотеза включает предположение о том, что в результате эксперимента возрастут или уменьшатся индивидуальные различия между испытуемыми. Такое предположение хорошо проверяется с помощью критерия Фишера, позволяющего сравнить дисперсии до и после эксперимента. Заметим, что, пользуясь критерием Фишера, можно работать только с абсолютными значениями показателей, но не с их рангами.

Результаты количественного и качественного анализа материала, полученного в ходе проведения эксперимента, первичной и вторичной статистической обработки этого материала, используются для доказательства правильности предложенных гипотез. Выводы об их истинности являются логическим следствием доказательства, в процессе которого в качестве основного аргумента выступает безупречность логики самого доказательства, а в качестве фактов - то, что установлено в результате количественного и качественного анализа экспериментальных данных.

Факты в ходе доказательства обязательно должны соотноситься с гипотезами. В процессе такого соотнесения выясняется, насколько полно имеющиеся факты доказывают, подтверждают предложенные гипотезы. (7)

Литература

1.         Годфруа Ж. Что такое психология: В 2-х т. Т.2: Пер. с франц. - М.: Мир, 1992. - 376 с.

2.         Горбатов Д.С. Практикум по психологическому исследованию: Учеб. пособие. - Самара: "БАХРАХ - М", 2003. - 272 с.

3.         Дружинин В.Н. Экспериментальная психология: Учебное пособие - М.: ИНФРА-М, 1997. - 256 с.

4.         Дружинин В.Н. Экспериментальная психология - СПб: Питер, 2000. - 320с.

5.         Ермолаев А.Ю. Математическая статистика для психологов. - М.: Московский психолого-социальный институт: Флинта, 2003.336с.

6.         Корнилова Т.В. Введение в психологический эксперимент. Учебник для ВУЗов. М.: Изд-во ЧеРо, 2001.

7.         Немов Р.С. Психология. Кн.3: Психодиагностика. Введение в научное психологическое исследование с элементами математической статистики. - М.: ВЛАДОС, 1998. – 632 с.