Курсовая работа: Модель производственной функции для сельскохозяйственной отрасли

Курсовая работа: Модель производственной функции для сельскохозяйственной отрасли

ВВЕДЕНИЕ

Производственная функция занимает важное место в экономической теории как модель, непосредственно относящаяся не к процессу обмена, а к процессу производства, который связан с потреблением различных ресурсов (сырье, энергия, труд, оборудование и т.д.).

Построение производственных функции, то есть выявление фактических технологических взаимосвязей в производстве, является одной из важнейших эконометрических задач. Экономический анализ производства исследует отношение между затратами и выпуском. Это отношение, и определяет максимальный объём выпуска при определенных комбинациях факторов производства.

Исследование производственной функции применяется в различных областях знаний и для широкого типа данных. Функции могут относиться к технологическим процессам в промышленности или сельском хозяйстве. При работе с производственной функцией возникают различные проблемы: выбор надлежащих объясняющих переменных, подготовка соответствующих данных, выбор математической функции, статистическая оценка, интерпретация результатов. Рассмотрение двух факторов производства обосновано при анализе промышленного производства, как предприятия, отрасли, так и национального, мирового хозяйств. Особый интерес для исследования представляет сельское хозяйство.

Сельскохозяйственная отрасль на мой взгляд является одной из базовой отраслью развитого государства, которая занимается выращиванием различных зерновых культур (а Украина как известно является одним из основных экспортеров зерна, пшеницы и др. зерновых культур). В условиях НТП (научно-технического прогресса) роль сельского хозяйства возрастает в связи с развитием технологий выращивания, с развитием и совершенствованием сельскохозяйственной техники и ростом населения, все это обуславливает интенсивное производство и как следствие потребление продукции сельского хозяйства.

И именно поэтому, в этой курсовой работе я решил попытаться разработать модель производственной функции для сельскохозяйственной отрасли.

Для исследования были использованы данные по валовой стоимости продукции в сельском хозяйстве Украины за 20 лет (1986 – 2007) относительно рабочей силы (L) и капитала (K).

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Понятие производственной функции

Производственная функция – это функция, независимая переменная которой принимает значения объёмов затрачиваемого или используемого ресурса (фактора производства), а зависимая переменная – значения объёмов выпускаемой продукции.

                                                                                          (1)

В формуле (1)  и  - числовые величины, т. е.  есть функция одной переменной . В связи с этим ПФ  называется одно-ресурсной или однофакторной ПФ, её область определения – множество неотрицательных действительных чисел (т. е. ). Запись  означает, что если ресурс затрачивается или используется в количестве  единиц, то продукция выпускается в количестве  единиц. Символ  - знак функции – является характеристикой производственной системы, преобразующей ресурс в выпуск. Символ  связывает между собой независимую переменную  с зависимой переменной . В макроэкономической теории принято считать, что  - это максимально возможный объём выпуска продукции, если ресурс затрачивается или используется в количестве  единиц. В макроэкономике такое понимание не совсем корректно: возможно, при другом распределении ресурсов между структурными единицами экономики выпуск мог бы быть и большим. В этом случае ПФ – это статистически устойчивая связь между затратами ресурса и выпуском. Более правильной является символика , где  - вектор параметров ПФ.

ПФ могут иметь различные области использования. Принцип «затраты – выпуск» может быть реализован как на микро - так и на макроэкономическом уровне. Сначала остановимся на микроэкономическом уровне. ПФ  может быть использована для описания взаимосвязи между величиной затрачиваемого или используемого ресурса  в течение года на отдельном предприятии и годовым выпуском продукции  этого предприятия. На микроэкономическом уровне в роли производственной системы может выступать также отрасль, межотраслевой производственный комплекс. МИПФ строятся и используются в основном для решения задач анализа и планирования, а также задач прогнозирования.

ПФ может быть использована для описания взаимосвязи между годовыми затратами труда в масштабе региона или страны в целом и годовым конечным выпуском продукции (или доходом) этого региона или страны в целом. Здесь в роли производственной системы выступает регион или страна в целом (точнее хозяйственная система региона или страны) – имеем макроэкономический уровень и макроэкономическую ПФ (МАПФ). МАПФ строятся и активно используются для решения всех трёх типов задач (анализа, планирования и прогнозирования).

Точное толкование понятий затрачиваемого (или используемого) ресурса и выпускаемой продукции, а также выбор единиц их измерения зависят от характера и масштаба производственной системы, особенностей решаемых (с помощью ПФ) задач (аналитических, плановых, прогнозных), наличия исходных данных. На микроэкономическом уровне затраты и выпуск могут измеряться как в натуральных, так и в стоимостных единицах (показателях). Годовые затраты труда могут быть измерены в человеко-часах (объём человеко-часов – натуральный показатель) или в рублях выплаченной заработной платы (её величина – стоимостной показатель). Выпуск продукции может быть представлен в штуках или в других натуральных единицах (тоннах, метрах и т. п.) или в виде своей стоимости.

На макроэкономическом уровне затраты и выпуск измеряются, как правило, в стоимостных показателях и представляют собой стоимостные (ценностные) агрегаты, т. е. суммарные величины произведений объёмов затрачиваемых (или используемых) ресурсов и выпускаемых продуктов на их цены.

Производственная функция (ПФ) – это модель, которая выражает технологическую зависимость между результатами деятельности технического объекта и затратами факторов производства. Входными параметрами являются ресурсы R1, ..., Rn, а выходными - результат в виде годовых объемов производства различных видов продукции Y1, ..., Ym .

В качестве ресурсов (факторов производства) наиболее часто рассматриваются величины затрат живого труда, предметов и средств труда, используемых в процессе производства: накопленный труд в форме производственных фондов (капитал) К и настоящий (живой) труд. В качестве результата рассматривается валовой выпуск (либо валовой внутренний продукт, либо национальный доход).

Простейшей моделью производственной функции является:

Y – выход;

K – капитал;

L – трудовые ресурсы.

Таким образом, экономика замещается своей моделью в форме ПФ

Y= F(K, L),

т.е. выпуск (продукции) есть функция от затрат ресурсов (капитала и труда).

Если модель учитывает время t затрат на производство, то производственная функция записывается в виде:

Y = F(K, L, t)

Производственная функция должна удовлетворять следующим условиям, поддающимся естественной экономической интерпретации:

1) F(K, L) – непрерывная дважды дифференцируемая функция в области K>0;

2) ,

-  с ростом ресурсов выпуск растет;

- 

3) ,

-  с увеличением ресурсов скорость роста выпуска замедляется;

Темпы прироста часто убывают при увеличении какого-либо фактора, особенно, если производство ведется по какой-либо неизменной технологии. Убывание темпов роста при увеличении масштабов производства часто связано с вынужденным использованием более дорогих или менее качественных ресурсов. При этом при достижении определенного уровня инвестиций в производство какого-нибудь отдельного фактора рост производства прекращается полностью, несмотря на увеличение рассматриваемого фактора.

4) F(lK, lL) = lF(K, L)

- гипотеза однородности

5) F(0, L) = F(K, 0) = 0

- при отсутствии одного из ресурсов производство невозможно;

6)  для F(K, L, t)

Виды производственных функций

Рассмотрим 4 производственные функции:

1. Линейная модель (функция с взаимозамещением ресурсов), задается уравнением:

Y = a0 + b1K + c1L,

где b1, c1 >0 – частные эффективности ресурсов (предельный физический продукт затрат)

2. Квадратичная модель, задается уравнением:

Y = a0 + b1K + c1L + b2K2 + c2L2

3. Модель Кобба-Дугласа, задается уравнением:

Y = AKaLb,

где А — коэффициент нейтрального технического прогресса; а1, a2 -коэффициенты эластичности по труду и капиталу.

4. Модель с учетом НТП, задается уравнением:

Y = AKaLber0t,

где  - специальный множитель технического процесса, r0 – параметр нейтрального НТП (r0 >0)

Параметры функции могут быть определены по методу наименьших квадратов

1. Для линейной модели:

Функция неувязок:

G =  = ® min по а0, b1, c1

Производные по коэффициентам:

, где i = 1…n

приравниваем нулю

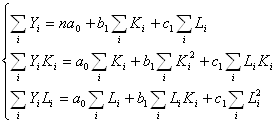                                                         (1)

2. Для квадратичной модели:

Функция неувязок:

G =  = ® min по а0, b1, c1, b2, c2

Производные по коэффициентам:

, где i = 1…n

приравниваем нулю

               (2)

3. Для модели Кобба-Дугласа:

Прологарифмируем функцию:

lnY = lnA + alnK + blnL

Функция неувязок:

G =  = ® min по A, a, b

Частные производные по коэффициентам:

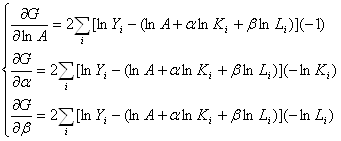, где i = 1…n

приравниваем нулю

 (3)

4. Для модели с учетом НТП:

Прологарифмируем функцию:

lnY = lnA + alnK + blnL + r0t

Функция неувязок:

G =  = ® min по A, a, b, r0

Частные производные по коэффициентам:

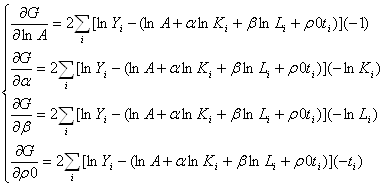, где i = 1…n

приравниваем нулю

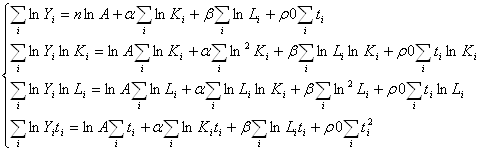       (4)

Далее из полученных уравнений находим неизвестные коэффициенты

ПРАКТИЧЕСКАЯ ЧАСТЬ

Исходные данные для построения ПФ

Годы	Y, Валовая стоимость продукции, млн. руб.	K, Капитал, млн. руб.	L, Расходы по з/п, млн. руб.
1987	3,626	12,021	1,251
1988	4,014	13,787	1,321
1989	4,453	15,429	1,392
1990	4,869	17,212	1,454
1991	5,296	19,042	1,507
1992	5,798	20,79	1,568
1993	6,233	23,097	1,598
1994	6,641	25,108	1,626
1995	7,241	27,097	1,667
1996	7,854	29,627	1,706
1997	8,09	32,362	1,753
1998	8,504	35,391	1,778
1999	8,879	38,474	1,806
2000	9,053	41,779	1,813
2001	9,11	45,976	1,855
2002	9,321	50,354	1,878
2003	9,545	55,018	1,898
2004	9,539	58,733	1,906
2005	9,774	61,935	1,911
2006	9,955	66,467	1,926
2007	10,1	69,488	1,939

Построение производственной функции

Линейная производственная функция

Построим линейную производственную функцию вида:

                                                                    (1)

где K – затраты капитала; L – расходы по заработной плате. И функция неувязок имеет вид

Анализируем исходные данные с помощью «Поиск решения» Microsoft Excel 2003. В результате получаем следующие показатели: Функция неувязок

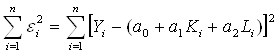
достигает минимума при

a0	a1	a2
-8,384563	0,0112465	9,15343789

Годы	K	L	Y	Y^	(Y-Y^)^2
1987	12,021	1,251	3,626	3,201583	0,180130129
1988	13,787	1,321	4,014	3,862185	0,023047917
1989	15,429	1,392	4,453	4,530545	0,006013299
1990	17,212	1,454	4,869	5,118111	0,062056363
1991	19,042	1,507	5,296	5,623824	0,107468886
1992	20,79	1,568	5,798	6,201843	0,163089243
1993	23,097	1,598	6,233	6,502392	0,072572016
1994	25,108	1,626	6,641	6,781305	0,019685475
1995	27,097	1,667	7,241	7,178965	0,003848315
1996	29,627	1,706	7,854	7,564403	0,083866442
1997	32,362	1,753	8,09	8,025374	0,004176551
1998	35,391	1,778	8,504	8,288275	0,046537103
1999	38,474	1,806	8,879	8,579245	0,089853262
2000	41,779	1,813	9,053	8,680488	0,138764849
2001	45,976	1,855	9,11	9,112134	4,55595E-06
2002	50,354	1,878	9,321	9,371901	0,002590889
2003	55,018	1,898	9,545	9,607423	0,003896665
2004	58,733	1,906	9,539	9,722432	0,033647144
2005	61,935	1,911	9,774	9,80421	0,00091265
2006	66,467	1,926	9,955	9,992481	0,001404816
2007	69,488	1,939	10,1	10,14545	0,002065819

Следовательно, теперь мы можем построить ПФ:

Y^ = -8,384563 + 0,0112465*K +9,15343789*L

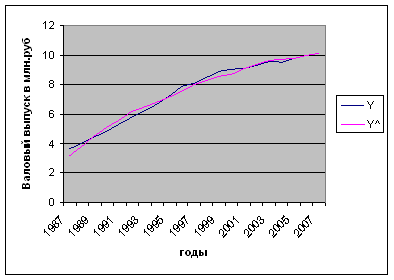
Рис.1 Графическое представление результатов аппроксимации производственной функции

Квадратичная производственная функция

Построим квадратичную производственную функцию вида:

                                          (2)

где K – затраты капитала; L – расходы по заработной плате. И функция неувязок имеет вид

Анализируем исходные данные с помощью «Поиск решения» Microsoft Excel 2003. В результате получаем следующие показатели:

Функция неувязок достигает минимума при:

a0	a1	a2	a3	a4
10,65719	-0,02671	-16,62825	-0,00006	8,9660141

Годы	K	L	Y	Y^	(Y-Y^)^2
1987	12,021	1,251	3,626	3,556971	0,004765067
1988	13,787	1,321	4,014	3,957216	0,003224444
1989	15,429	1,392	4,453	4,456814	1,45478E-05
1990	17,212	1,454	4,869	4,956672	0,007686313
1991	19,042	1,507	5,296	5,429411	0,017798428
1992	20,79	1,568	5,798	6,045845	0,06142728
1993	23,097	1,598	6,233	6,330639	0,009533385
1994	25,108	1,626	6,641	6,614652	0,000694191
1995	27,097	1,667	7,241	7,083803	0,024710798
1996	29,627	1,706	7,854	7,538203	0,099727837
1997	32,362	1,753	8,09	8,130652	0,001652609
1998	35,391	1,778	8,504	8,412681	0,00833908
1999	38,474	1,806	8,879	8,750258	0,016574426
2000	41,779	1,813	9,053	8,756131	0,08813129
2001	45,976	1,855	9,11	9,303874	0,037587284
2002	50,354	1,878	9,321	9,547923	0,051493886
2003	55,018	1,898	9,545	9,737155	0,036923633
2004	58,733	1,906	9,539	9,751322	0,045080747
2005	61,935	1,911	9,774	9,729603	0,001971064
2006	66,467	1,926	9,955	9,838768	0,013509783
2007	69,488	1,939	10,1	9,966716	0,017764679

Следовательно, ПФ имеет вид:

Y^ = 10,65719 - 0,02671*K - 16,62825*L - 0,00006*K2 + 8,9660141*L2

 

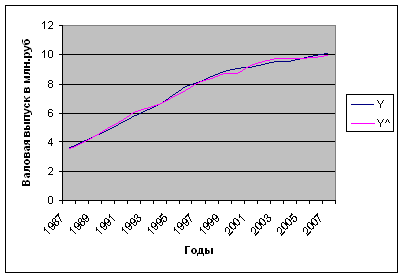
Рис.2 Графическое представление результатов аппроксимации производственной функции

Производственная функция Кобба-Дугласа

Производственная функция Кобба-Дугласа при

Построим производственную функцию Кобба-Дугласа вида:

,                                                                                  (3)

где K – затраты капитала; L – расходы по заработной плате, при α+β=1. И функция неувязок имеет вид

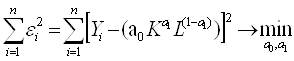
Анализируем исходные данные с помощью «Поиск решения» Microsoft Excel 2003. В результате получаем следующие показатели:

A
1,51428	0,358355	0,641646

Годы	K	L	Y	Y^	(Y-Y^)^2
1987	12,021	1,251	3,626	4,261998	0,404493704
1988	13,787	1,321	4,014	4,635727	0,386545002
1989	15,429	1,392	4,453	4,991358	0,289829368
1990	17,212	1,454	4,869	5,338037	0,219995285
1991	19,042	1,507	5,296	5,663481	0,135042394
1992	20,79	1,568	5,798	5,995276	0,038917787
1993	23,097	1,598	6,233	6,301843	0,004739403
1994	25,108	1,626	6,641	6,565998	0,005625294
1995	27,097	1,667	7,241	6,85654	0,147809652
1996	29,627	1,706	7,854	7,185243	0,447235307
1997	32,362	1,753	8,09	7,546696	0,295179318
1998	35,391	1,778	8,504	7,863713	0,409967528
1999	38,474	1,806	8,879	8,18429	0,482621959
2000	41,779	1,813	9,053	8,450547	0,36295021
2001	45,976	1,855	9,11	8,874924	0,055260868
2002	50,354	1,878	9,321	9,241757	0,006279478
2003	55,018	1,898	9,545	9,604897	0,003587687
2004	58,733	1,906	9,539	9,859026	0,102416413
2005	61,935	1,911	9,774	10,06527	0,084839983
2006	66,467	1,926	9,955	10,37517	0,176539605
2007	69,488	1,939	10,1	10,58735	0,237509292

ПФ примет следующий вид:

Y^ = 1,51428*K 0,358355 *L 0,641646

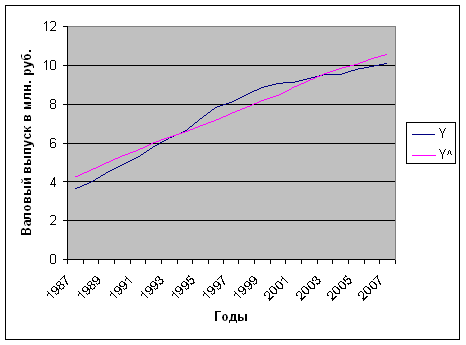
Риc. 3 Графическое представление результатов аппроксимации производственной функции

Производственная функция Кобба-Дугласа при

Построим производственную функцию Кобба-Дугласа вида:

,                                                                                  (4)

где K – затраты капитала; L – расходы по заработной плате, при α+β≠1.

и функция неувязок имеет вид

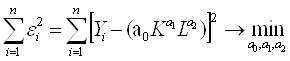
Анализируем исходные данные с помощью «Поиск решения» Microsoft Excel 2003.

В результате получаем следующие показатели:

Функция неувязок 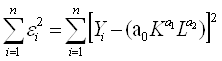достигает минимума при:

A
1,897142	0,00058832	2,549475

Годы	K	L	Y	Y^	(Y-Y^)^2
1987	12,021	1,251	3,626	3,362716	0,069318534
1988	13,787	1,321	4,014	3,863748	0,022575574
1989	15,429	1,392	4,453	4,41574	0,001388299
1990	17,212	1,454	4,869	4,934927	0,004346316
1991	19,042	1,507	5,296	5,406895	0,012297621
1992	20,79	1,568	5,798	5,982806	0,03415343
1993	23,097	1,598	6,233	6,279367	0,002149873
1994	25,108	1,626	6,641	6,564019	0,005926094
1995	27,097	1,667	7,241	6,994586	0,060719804
1996	29,627	1,706	7,854	7,419767	0,1885579
1997	32,362	1,753	8,09	7,952506	0,018904497
1998	35,391	1,778	8,504	8,245287	0,06693267
1999	38,474	1,806	8,879	8,5808	0,088922973
2000	41,779	1,813	9,053	8,666268	0,149561493
2001	45,976	1,855	9,11	9,187851	0,006060771
2002	50,354	1,878	9,321	9,481589	0,025788929
2003	55,018	1,898	9,545	9,741659	0,038674906
2004	58,733	1,906	9,539	9,847063	0,094903007
2005	61,935	1,911	9,774	9,913364	0,019422386
2006	66,467	1,926	9,955	10,11337	0,025082505
2007	69,488	1,939	10,1	10,28859	0,035565711

В результате ПФ будет иметь следующий вид:

Y^ = 1,897142*K 0,00058832 *L 2,549475

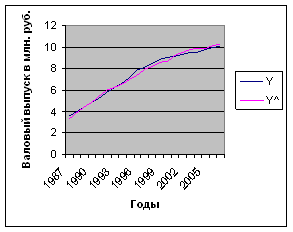
Рис.4 Графическое представление результатов аппроксимации производственной функции

Производственная функция Кобба-Дугласа с учетом НТП при

Построим производственную функцию Кобба-Дугласа с учётом НТП вида:

,                                                                 (5)

где K – затраты капитала; L – расходы по заработной плате, – специальный множитель технического прогресса, p0 – параметр нейтрального НТП (p0>0) при α+β=1. И функция неувязок имеет вид

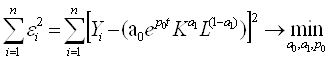
Анализируем исходные данные с помощью «Поиск решения» Microsoft Excel 2003.

В результате получаем следующие показатели:

Функция неувязок достигает минимума при:

A			p
1,11077	0,49463	0,50537	-0,009

t	Годы	K	L	Y	Y^	(Y-Y^)^2
0	1987	12,021	1,251	3,626	4,255462	0,396223037
1	1988	13,787	1,321	4,014	4,639196	0,390869685
2	1989	15,429	1,392	4,453	4,99121	0,289670078
3	1990	17,212	1,454	4,869	5,33781	0,219782385
4	1991	19,042	1,507	5,296	5,662748	0,134504095
5	1992	20,79	1,568	5,798	5,980033	0,033136038
6	1993	23,097	1,598	6,233	6,303323	0,004945302
7	1994	25,108	1,626	6,641	6,567753	0,005365166
8	1995	27,097	1,667	7,241	6,844795	0,156978794
9	1996	29,627	1,706	7,854	7,173191	0,463500994
10	1997	32,362	1,753	8,09	7,529158	0,314544001
11	1998	35,391	1,778	8,504	7,855534	0,420508573
12	1999	38,474	1,806	8,879	8,178033	0,491354634
13	2000	41,779	1,813	9,053	8,458675	0,35322206
14	2001	45,976	1,855	9,11	8,891876	0,047577972
15	2002	50,354	1,878	9,321	9,275526	0,002067921
16	2003	55,018	1,898	9,545	9,65592	0,012303177
17	2004	58,733	1,906	9,539	9,904998	0,133954245
18	2005	61,935	1,911	9,774	10,09099	0,100483383
19	2006	66,467	1,926	9,955	10,39732	0,195646721
20	2007	69,488	1,939	10,1	10,56933	0,220267427

ПФ будет иметь следующий вид:

Y^ = 1,11077*e -0,009t *K 0,49463 *L 0,50537

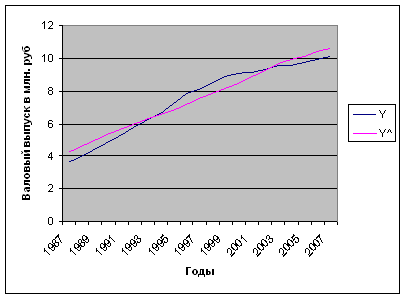
Рис. 5 Графическое представление результатов аппроксимации производственной функции

Производственная функция Кобба-Дугласа с учетом НТП при

Построим производственную функцию Кобба-Дугласа с учётом НТП вида:

,                                                                     (6)

где K – затраты капитала; L – расходы по заработной плате, – специальный множитель технического прогресса, p0 – параметр нейтрального НТП (p0>0) при α+β≠1. И функция неувязок имеет вид

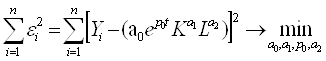
Анализируем исходные данные с помощью «Поиск решения» Microsoft Excel 2003.

В результате получаем следующие показатели:

Функция неувязок 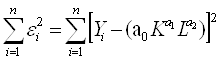достигает минимума при:

А			p
1,6643	0,03954	2,72382	-0,0087

t	Годы	K	L	Y	Y^	(Y-Y^)^2
0	1987	12,021	1,251	3,626	3,379381	0,060820827
1	1988	13,787	1,321	4,014	3,90663	0,01152829
2	1989	15,429	1,392	4,453	4,486108	0,001096134
3	1990	17,212	1,454	4,869	5,029232	0,025674263
4	1991	19,042	1,507	5,296	5,51816	0,049355124
5	1992	20,79	1,568	5,798	6,115709	0,100939186
6	1993	23,097	1,598	6,233	6,410297	0,031434332
7	1994	25,108	1,626	6,641	6,684439	0,001886985
8	1995	27,097	1,667	7,241	7,112754	0,016447068
9	1996	29,627	1,706	7,854	7,535854	0,10121715
10	1997	32,362	1,753	8,09	8,072406	0,000309535
11	1998	35,391	1,778	8,504	8,346336	0,024857912
12	1999	38,474	1,806	8,879	8,662023	0,047078837
13	2000	41,779	1,813	9,053	8,705948	0,120444823
14	2001	45,976	1,855	9,11	9,220546	0,012220454
15	2002	50,354	1,878	9,321	9,486389	0,027353667
16	2003	55,018	1,898	9,545	9,713119	0,028264079
17	2004	58,733	1,906	9,539	9,764764	0,050969488
18	2005	61,935	1,911	9,774	9,769625	1,91375E-05
19	2006	66,467	1,926	9,955	9,920761	0,001172281
20	2007	69,488	1,939	10,1	10,03394	0,004364053

ПФ будет иметь следующий вид:

Y^ = 1,6643*e -0,0087 *K 0,03954 *L 2,72382

 

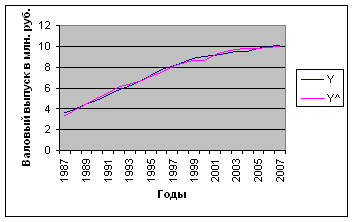
Рис. 6 Графическое представление результатов аппроксимации производственной функции

Выбор лучшей модели

В предыдущей главе нами были построены и рассмотрены шесть видов производственной функции. Для построения прогноза уровня валовой стоимости продукции по с/х отрасли Украины для следующего года необходимо выбрать оптимальную модель производственной функции.

Для этого анализируем исходные данные с помощью линейного регрессионного анализа Microsoft Excel 2003, который заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов.

В результате получаем следующие показатели:

Модель производственной функции	Коэффициент детерминации	Стандартная ошибка	Сумма квадратов отклонений
Линейная	1,00	4,91*10-11	1,045632392
Кобба-Дугласа при α+β=1	0,999651913009379	0,0390553466664897	4,297385537
Кобба-Дугласа при α+β≠1	0,9986565670686	0,0849838692196464	0,971253293
Кобба-Дугласа с учётом НТП при α+β=1	0,999434169760968	0,0500555152681243	4,386905687
Кобба-Дугласа с учётом НТП при α+β≠1	0,998312036260028	0,0924459064874472	0,717453627
Квадратичная	0,994458953118657	0,167341009587636	0,54886177

Критерий выбора следующий: наибольшее значение коэффициента детерминации , наименьшая ошибка и наименьшая сумма квадратов отклонений.

Таким образом, для данной отрасли мы выбираем производственную функцию Кобба-Дугласа при α+β=1, которая выглядит следующим образом:

Y^ = 1,51428*K 0,358355 *L 0,641646

Полученная модель может быть использована для прогнозирования будущих значений валовой стоимости продукции на основе известных или ожидаемых уровнях капитала и затрат на заработную плату.

Расчет экономических характеристик выбранной производственной функции

Итак, процесс производства описывается с помощью функции Кобба-Дугласа при α+β=1

Y^ = 1,51428*K 0,358355 *L 0,641646

Оценим основные характеристики этой функции для способа производства, при котором К=75 млн. руб., а L=2,5млн. руб.:

Эластичность выпуска продукции по капиталу и труду

Эластичность выпуска продукции по капиталу и труду равна соответственно a и b, так как

,

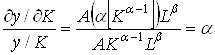и аналогичным образом легко показать, что (dy/dL)/(y/L) равно b.

Следовательно, увеличение затрат капитала на 1% приведет к росту выпуска продукции на 0,358355 процента, а увеличение затрат труда на 1% приведет к росту выпуска на 0,641646 процентов. Эти величины a=0,358355 и b=0,641646 положительны, следовательно увеличение затрат производственных факторов должно вызывать рост выпуска. В то же время, они меньше единицы, и разумно предположить, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторы остаются постоянными. Их сумма равна единице, и это говорит о постоянном эффекте от масштаба производства (y увеличивается в той же пропорции, что и К и L).

Производительность труда

Производительность труда показывает степень результативности использования трудовых ресурсов и вычисляется по формуле . Для нашего примера производительность труда будет равна

Фондоотдача

Фондоотдача (капиталоотдача) характеризует уровень плодотворности применения основного капитала (основных фондов) и вычисляется по формуле . Для нашего примера фондоотдача будет равна:

Предельная производительность труда и капитала

Для расчета этих величин определим частные производные функции по каждому из факторов:

 – предельная производительность труда

 – предельная производительность капитала

Таким образом, увеличение затрат капитала на 1 единицу при неизменных объемах используемого труда приведет к росту выпуска продукции на 0,061197 единицу, а увеличение затрат труда на 1 единицу при неизменных объемах капитала приведет к росту выпуска на 3,287271 единиц. И предельная производительность труда в три раза превышает аналогичную величину для фактора капитал.

Предельная норма замещения труда капиталом

Эта величина обозначается S и равняется . И для нашей функции предельная норма замещения ресурсов будет равна:

Таким образом, если затраты труда уменьшатся на 1 единицу, то при неизменном выпуске продукции затраты капитала увеличатся на 53,71613 единицы.

ЗАКЛЮЧЕНИЕ

В ходе выполнения данной курсовой работы были построены и проанализированы различные модели производственных функций на основе данных, отражающих сельскохозяйственную отрасль Украины, с использованием стандартного набора факторов (капитальные затраты и расходы по заработной плате) позволяющие оценить и получить некоторое представление о взаимном влиянии объясняемой (Y) и объясняющих переменных (Х1, Х2).

Построение производственных функций помогло нам рассмотреть эффективность применения определённой комбинации ресурсов. В итоге можно сделать вывод, что расходы по заработной плате, так же, как и затраты капитала несомненно влияют на отраслевой выпуск продукции, ведь от условий производства зависит то, каким образом отрасль будет позиционировать себя и то насколько успешно будет её деятельность.

Стоит отметить, что без эконометрических методов в экономике невозможно построить надёжного прогноза, а, следовательно, подвергается угрозе экономическая эффективность и возможность дальнейшего развития, как отдельного предприятия, так и системы национального хозяйства.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.  Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: Юнити-Дана, 2003.

2.  Мхитарян В.С., Архипова М.Ю., Сиротин В.П. Эконометрика: Учебно-методический комплекс. – М.: Изд. Центр ЕАОИ. 2008. – 144с.

3.  Статистический ежегодник Украины, 1986-2007гг.

4.  Калинина В.Н. Соловьев В.И. Практикум по эконометрическому моделированию. - М.: Юнити-Дана, 2008.

5.  Волков А.В. Математическая экономика. – М.: Изд. Центр РЭА им. Плеханова, 2008.

ИНТЕРНЕТ-РЕСУРСЫ

1.  http://www.prime-tass.ru/

2.  www.ukrstat.gov.ua

3.  http://www.expert.ru/