Реферат: Математические модели формирования и использования запасов

Реферат: Математические модели формирования и использования запасов

 

 

 

 

 

 

 

 

 

 

 

Математические модели формирования и использования запасов

 

Введение

Запасы средств производства представляют собой экономическую категорию, присущую товарному производству на всех стадиях его развития. Они призваны обеспечить непрерывность и высокие темпы расширенного воспроизводства.

Возникает вопрос: зачем же обществу нужны запасы? Существует много причин, почему организации идут на их создание. Основной довод состоит в том, что обычно либо физически невозможно, либо экономически невыгодно, чтобы товары поступали именно тогда, когда на них возникает спрос. При отсутствии запасов потребителям приходилось бы ждать, пока их заказы будут выполнены. Однако обычно потребители не хотят или не могут долго ждать. Одно это говорит о необходимости хранения запасов почти каждой организацией, снабжающей товарами потребителей. Но существуют и другие причины для создания запасов. К ним относятся цены на сырье, которые могут подвергаться значительным сезонным колебаниям. Когда цена низка, выгодно создавать достаточные запасы сырья, которых хватило бы на весь сезон высоких цен, которые можно было бы по мере надобности использовать в производстве. Другой довод, особенно важный для предприятий розничной торговли, состоит в том, что объем продаж и прибыль могут быть увеличены, если имеется некоторый запас товаров, который можно предложить потребителю.

И хотя вопросы, связанные с хранением запасов, столь же стары, как и сама история, только с начала 20 века были сделаны попытки использовать аналитические методы для их изучения. Первоначальным толчком к применению математических методов анализа систем управления запасами послужило, вероятно, одновременное развитие промышленности и технических наук, и особенно науки об организации производства. Реальную потребность в анализе впервые ощутили те отрасли промышленности, которым пришлось столкнуться с вопросами календарного планирования производства и хранения запасов, когда продукция производится серийно и поступает на заводской склад.

Впервые вывод формулы, которую часто называют простой формулой размера партии, был сделан Фордом Харрисом в 1915 году. С тех пор эта же самая формула была получена, вероятнее всего самостоятельно, многими исследователями. Часто ее называют формулой Уилсона, так как она была получена в качестве одного из результатов разработанной Уилсоном схемы управления запасами.

И лишь по окончании второй мировой войны, когда стали развиваться наука о методах управления и руководства и исследование операций, было обращено серьезное внимание на случайный характер процессов управления запасами. До этого системы рассматривались как детерминированные, за исключением тех немногих случаев, как, например, работа Уилсона, где были сделаны попытки как-то учесть вероятностный характер этих систем.

Интерес к использованию аналитических методов решения задач управления запасами впервые возник в промышленности, где инженеры искали способы решения практических задач.

В настоящее время работы в этой области ведутся в различных аспектах. С одной стороны, значительная работа проводится непосредственно в области практического применения, хотя с другой стороны, исследуются и абстрактные математические свойства моделей управления запасами.

При управлении запасами любого товара следует ответить на два основных вопроса: когда пополнить запас, и каков должен быть размер заказа на пополнение?

 

1 Построение модели управления запасами в условиях детерминированного спроса

 

1.1 Оптимальные партии поставки для однопродуктовых моделей

Модель управления запасами в условиях детерминированного спроса – это модель где интенсивность поступления требований предполагается известной и постоянной во времени. Как известно, на практике спрос почти никогда нельзя указать с определенностью; вместо этого его следует описывать в вероятностных терминах.

Детерминированные модели интересны тем, что позволяют познакомиться с методами анализа, используемыми в более сложных системах. Кроме того, результаты, полученные с помощью этих моделей, дают качественно правильные суждения о поведении системы даже при отказе от гипотезы детерминированного спроса.

На рис.1.1. показан самый общий случай образования (ОА), расходования (АК) запаса, затем возможное образование дефицита (КD) и его удовлетворения (DS). В точке S вновь начинается формирование запаса, так что временной отрезок OS представляет собой продолжительность рассмотренного цикла.

Рис. 1.1. Схема движения запасов для детерминированного спроса

Таким образом, на рис.4.1. показана схема однопродуктовой модели с учетом неудовлетворенных требований и конечной интенсивностью потребления и расходования запаса, где по оси ординат откладывается величина текущего запаса I, а по оси абсцисс – время t.

Обозначим:

l – интенсивность поступления;

n – постоянная интенсивность потребления;

t1 – продолжительность формирования запаса со скоростью l [ед. запаса/ ед. времени];

t2 – время расходования запаса со скоростью n;

t3 – время образования дефицита со скоростью n;

t4 – время погашения дефицита со скоростью l.

Тогда (l-n) – интенсивность (скорость) пополнения запаса.

Максимальный уровень (объем) наличного запаса AB=Y составит:

математическая модель оптимальный запасы

Максимальный уровень дефицита ED=y составит:

Продолжительность цикла поставки очередной партии или время возобновления запаса :

Так как спрос удовлетворяется полностью, но не всегда своевременно, то величина партии поставки:

Выразив ,  и  через  и  из (4-1) и (4-2) соответственно, получим:

Общие издержки при работе этой системы обеспечения запасами складываются из:

· издержек  от размещения запасов, которые не зависят от величины ;

· издержек от содержания запасов ;

· издержек от наличия дефицита .

Величина:

где  – удельные расходы на хранение и иммобилизацию средств

[ руб./ ед. 60 минут].

Потери из-за отсутствия продукции, на которую предъявляются требования, или от дефицита считаем пропорциональными средней величине задолженных требований и времени их осуществления:

где — удельные издержки дефицита, т.е. потери, связанные с нехваткой единицы продукции в единицу времени.

Учитывая полученные выражения ,  и , получим формулу для общих издержек в системе в течении цикла :

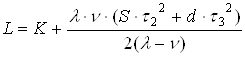
отсюда удельные издержки за цикл составят:

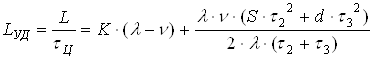
Найдем оптимальные значения τ2* и τ3* из условия, что:

            

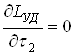
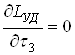
Условия (4-10) позволяют получить систему двух уравнений с двумя неизвестными  и :

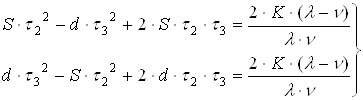
Обозначим  и разделим первое из уравнений системы (4-11) на второе, найдем:

.

Откуд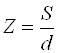а , и тогда

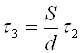
Подставив (4-12) в любое из уравнений системы (4-11), получим оптимальные значения:

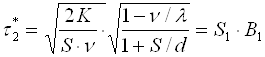
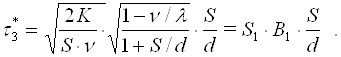
Учитывая (4-13) и (4-14), из (4-5) получим оптимальные значения еще двух составляющих продолжительности цикла возобновления запасов:

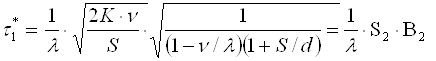
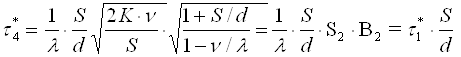
Подставив τ2* и τ2* в формулы (4-5) и (4-4), получим оптимальные значения цикла повторения заказа и партии однопродуктовой поставки:

τц*=√ 2·K/(S·n)·√(1+ S / d)/ (1-n/l)= S1/B1 (4-17)

q* = √ 2·K·n/S·√(1+ S / d)/ (1-n/l)= S2/B1 (4-18)

Аналогично, подставив значения τ2* и τ3* из (4-13) и (4-14) в (4-9), определим оптимальные удельные издержки системы:

Lуд*=√ 2·K·n·S√ (1-n/l)/(1+ S / d)= √ 2·K·n·S· B1 (4-19)

И, наконец, находим оптимальные значения максимального уровня наличного запаса и задолженного спроса:

Y*= √ 2·K·n/S·√ (1-n/l)/(1+ S / d)= √ 2·K·n/(S · B1) (4-20)

y*= S / d·√ 2·K·n/S·√ (1-n/l)/(1+ S / d)= S / d·√ 2·K·n/(S · B1 ) (4-21)

Общие оптимальные издержки системы за время возобновления запаса составят:

Lобщ *= Lуд* ·τц* (4-22)

Модель с учетом неудовлетворенных требований при конечной интенсивности поступлений можно широко применять при:

1.  управлении поставками материальных ресурсов;

2.  определении оптимальной величины запуска деталей в производство с учетом переналадок на одном и том же технологическом оборудовании.

Во втором случае K – это издержки, связанные с переналадками. Предполагается, что они не зависят от величины выпускаемой партии и порядка запуска деталей в производство, l – интенсивность выпуска (производительность), τ1+ τ4 – время, затраченное на производство определенного типа изделий.

Из уравнений (4-13) – (4-22) можно получить ряд других частных моделей:

a)  при большой интенсивности пополнения, когда вся заказанная партия поступает одновременно; это значит, что l>>n и тогда можно принять n/l®0.

b)  при больших штрафах за допущение дефицита S/d®0, т.е. дефицит недопустим (d>>S).

c)  когда пункты а) и b) действуют одновременно. т.е. n/l®0, S/d®0, тогда имеем:

q* = √ 2·K·n/S

τц*=√ 2·K/(S·n)

Lуд*=√ 2·K·n·S

Последняя модель в отечественной и зарубежной литературе получила название Уилсона.Применяя формулы (4-17) – (4-19), можно показать, что за счет разумного компромисса между затратами на содержание и потерями от дефицита можно уменьшить общие затраты в единицу времени в √1+S/d раз. При n/l®0 и высоких штрафах за дефицит рассматриваемая модель превращается в модель Уилсона.

 

1.2 Оптимальные партии поставки для многопродуктовых моделей

Также как и для однопродуктовых поставок, суммарные издержки от функционирования системы складываются из издержек размещения заказов, содержания запаса и убытков вследствие дефицита.

Суммарные издержки размещения заказа:

∑i Кi = К0(1+ γ·N)

где К0 – издержки, не зависящие от числа одновременно заказанных продуктов и размера партии поставки;

γ – доля издержек, учитывающая размещение заказа по каждому i-тому продукту;

N – число продуктов.

Правая часть формулы (4-23) используется для расчета оптимального поставочного комплекта. Если же рассчитываются оптимальные партии запуска деталей в производство, изготавливаемых на одном и том же оборудовании, тогда используется левая часть формулы (4-23), где Кi --издержки переналадок. Причем, Кi не зависят от последовательности запуска деталей в производство. Период возобновления заказов τц* одинаков для всех одновременно заказываемых N продуктов.

Для удельных издержек работы системы с учетом интенсивности поступления и потерь от дефицита (т.е. с учетом неудовлетворенных требований) справедлива формула:

Lуд = 1/ τц· ∑i Кi+0,5· τц·∑i[(1-ni / l i)/(1+ S i / d i)]

Взяв частную производную и приравняв к нулю ∂Lуд/∂ τц=0, получим:

τц* = √2· ∑i Кi / [∑i(S i·ni·(1-ni / l i)/(1+ S i / d i))]

Тогда можно найти оптимальные размеры партии запуска деталей в производство из формулы:

qi* = n i · τц*

Оптимальная величина удельных издержек, с учетом (4-24), составит:

Lуд * = √2· ∑i Кi · [∑i(S i·ni·(1-ni / l i)/(1+ S i / d i))] (4-27)

Минимизация издержек от переналадок достигается из условия:

∑i=1N(ni / l i)≤1 (4-28)

В общем случае ограничение по ресурсам можно отразить в формуле:

∑i aij · qi ≤ Aj, j=1,n (4-29)

где aij – расход соответствующего ресурса на единицу продукции;

Aj – величина ограничения по виду ресурса (норматив).

Если условие (4-29) не выполняется, то рассчитывается новое значение оптимального периода выпуска деталей или партии поставки из условия:

τ*= min{ƒ/(∑i ƒ i ·ni), A/(∑i α i ·ni)} (4-30),

где, например, первое ограничение относится к складским площадям, а второе – к оборотным средствам. И, далее, все параметры системы пересчитываются заново.

 

1.3 Определение оптимальных параметров системы управления движением запасов

Применим рассмотренную в 4.1 модель управления запасами к конкретному примеру, который заключается в следующем: на одном и том же оборудовании производится три типа полуфабрикатов.

Объект моделирования – склад готовой продукции, система управления движением запасов с учетом ограничений на складские помещения и оборотные средства.

Проблемная ситуация – определение оптимальных значений партии поставки полуфабрикатов, их максимального уровня запаса, времени производства, бездефицитной и дефицитной работы системы управления запасами для каждого вида полуфабрикатов при заданных условиях.

Наблюдаемые параметры:

·  стоимость переналадок оборудования Ki [ден. ед.], которая не зависит от очередности выпуска полуфабрикатов, отправляемых затем в неподалеку расположенные склады общей площадью F = 300 м²;

·  стоимость содержания единицы запаса полуфабрикатов Si
[ден. ед./ (ед. п/фабр.: ед. врем.)];

·  скорость поступления li [ ед. п/фабр.: (ед. врем.) ];

·  скорость расходования Vi [ ед. п/фабр.: (ед. врем.) ];

·  нормативы по складским помещениям fi [ м/(ед. п/фабр.) ];

·  нормативы по оборотным средствам ai [ ден. ед./ед. п/фабр.];

·  потери от дефицита di [ ден.ед./(ед. п/фабр.:ед. врем.) ];величина оборотных средств не должна превышать значения;

·  А0 = 20000 [ ден. ед.].

Ненаблюдаемые параметры:

1)  партии поставки полуфабрикатов qi* ;

2)  максимальный уровень запасов полуфабрикатов Yi* ;

3)  времени производства полуфабрикатов τпрi*;

4)  времени формирования запасов τi1*;

5)  времени ликвидации дефицита τi4*;

6)  времени расходования запаса τi2*;

7)  времени бездефицитной работы Hi* ;

8)  времени работы при наличие дефицита Ni* для каждого вида полуфабрикатов.

Адекватность – соответствие расчетных и фактических параметров системы управления движением запасов.

Математический аппарат – дифференциальное исчисление, частные производные, алгебраические уравнения.

Результат моделирования – организация системы оптимального управления запасами; оптимальные значения партии поставки полуфабрикатов qi* , максимальный уровень запасов полуфабрикатов Yi* ; времени производства полуфабрикатов τпрi*; времени формирования запасов τi1*; времени ликвидации дефицита τi4*; времени расходования запаса τi2*; времени бездефицитной работы Hi* ; времени работы при наличие дефицита Ni* для каждого вида полуфабрикатов (табл. 1.1.).

Таблица 1.1

Исходные данные по полуфабрикатам

I	Vi	li	Ki	Si	di	fi	ai
1	49	245	52	6	18	1,5	50
2	178	685	78	8	32	1,4	50
3	266	1520	43	10	20	2	100

Для решения данной задачи следует использовать модель с учетом неудовлетворенных требований многопродуктового производства.

В связи с этим предварительно рассчитываются вспомогательные данные:

Vi/li, Аi=1- Vi/li , Mi= S i / d i , Bi=1- S i / d i , R i= S i· Vi · Аi / Bi

Тогда оптимальное время возобновления поставок:

τц*=√2· ∑i Кi / [∑i(S i· Vi · Аi / Bi)]

Подставив числовые значения исходных данных, получим значения вспомогательных данных (табл. 1.2.).

Таблица 1.2

Значения вспомогательных данных

i	Аi	Mi	Bi	R i
1	0,8	0,33	0,67	351,05
2	0,74	0,25	0,75	1405,01
3	0,825	0,5	0,5	4389

Требуемые оптимальные параметры управления запасами вычислим по следующим формулам:

qi*= Vi ·τц*

τпрi*= qi*/li

τi1*= τпрi*/ Bi

τi4*= τпрi*- τi1*

τi2*= τц*· Аi / Bi (4-31)

Hi* = τi1*+ τi2*

Ni* = Hi*+ Mi

Yi* = qi·(1+ Vi)/li

Подставив числовые данные, получим (табл.1.3.):

Таблица 1.3

Оптимальные параметры системы управления запасами

I	qi*	τпрi*	τi1*	τi4*	τi2*	Hi*	Ni*	Yi*
1	11,61	0,05	0,07	0,02	0,28	0,35	0,68	2,37
2	42,19	0,06	0,08	0,02	0,23	0,31	0,56	11,02
3	63,04	0,04	0,08	0,04	0,39	0,47	0,97	11,07

Выполним проверку ограничений:

·  по складским помещениям

τF =F/∑i fi· Vi, τF = 0,35 ед. врем.

·  по оборотным средствам

τA= А0/∑i ai · Vi, τA= 0,53 ед. врем.

Поскольку τц* < τF < τA, то пересчет полученных оптимальных параметров (табл. 4.3.) не требуется.

Заключение

Системы управления материальными запасами играют важную роль в экономической системе, так как они обеспечивают надежность функционирования экономических объектов – предприятий, отраслей, транспорта.

В данном разделе рассмотрены математические модели управления запасами в условиях детерминированного спроса, которые применяются для управления поставками ресурсов и очередностью запуска деталей (полуфабрикатов) в производство с учетом переналадок на одном и том же технологическом оборудовании.

В качестве примера были рассчитаны оптимальные партии поставки для многопродуктовой модели при заданных исходных условиях.

В результате вычислений получены следующие параметры системы управления запасами:

1)  партии поставки полуфабрикатов qi*;

2)  максимальный уровень запасов полуфабрикатов Yi*;

3)  времени производства полуфабрикатов τпрi*;

4)  времени формирования запасов τi1*;

5)  времени ликвидации дефицита τi4*;

6)  времени расходования запаса τi2*;

7)  времени бездефицитной работы Hi*;

8)  времени работы при наличие дефицита Ni* для каждого вида полуфабрикатов.

Кроме того, установлены точные соответствия между продолжительностью цикла поставок τц* и основными характеристиками системы управления запасами.