Курсовая работа: Цифровая фототриангуляция для создания топографических карт
Курсовая работа: Цифровая фототриангуляция для создания топографических карт
Министерство образования Российской Федерации
Федеральное агенство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
Кафедра фотограмметрии и дистанционного зондирования
Курсовая работа по дисциплине “Автоматизированная обработка аэрокосмической информации”
на тему:
“Цифровая фототриангуляция для создания топографических карт”
Выполнил:
Ст. гр. ИП-41
Пашинский В.А.
Проверил:
Широкова Т.А
Новосибирск, 2008г
Содержание
Введение
1. Цифровая фототриангуляция
1.1 Сущность, классификация и назначение фототриангуляции
1.2 Достоинства цифровой фототриангуляции
1.3 Сущность основных методов цифровой и аналитической фототриангуляции
1.3.1 Метод независимых моделей
1.3.2 Построение блочных сетей фототриангуляции методом связок
1.3.3 Построение блочной сети фототриангуляции объединением одиночных моделей
1.3.4 Построение блочной сети фототриангуляции объединением независимых маршрутных моделей
1.4 Особенности цифровой фототриангуляции
2. Технология построения блочной сети фототриангуляции на ЦФС «Фотомод»
2.1 Краткая характеристика ЦФС «Фотомод»
2.2 Основные процессы технологии построения блочной сети фототриангуляции на ЦФС «Фотомод»
3. Построение блочной сети фототриангуляции на ЦФС «Фотомод»
3.1 Оценка фотографического и фотограмметрического качества исходных фотоматериалов
3.2 Составление рабочего проекта построения блочной сети ПФТ
3.3 Подготовка исходных данных для построения сети
3.4 Ввод параметров проекта
3.5 Внутреннее ориентирование снимков
3.6 Построение и уравнивание блочной сети фототриангуляции
3.7Оценка точности, контроль качества и анализ результатов цифровой фототриангуляции
4. Исследования точности построения блочной сети фототриангуляции с использование ЦФС «Фотомод»
Заключение
Список использованных источников
Введение
В настоящее время во всех фирмах, занимающихся фотограмметрической обработкой снимков, применяется цифровой способ фототриангуляции и соответствующие программные продукты. Поэтому целью данной курсовой работы является изучение теоретических основ и получение практических навыков построения сетей пространственной фототриангуляции по результатам аэрофотосъемки с использование программного продукта.
В данной курсовой работе в первом разделе будут рассмотрены понятие пространственной цифровой фототриангуляции, назначение, достоинства, основные методы, а также её особенности.
Во втором разделе будет рассмотрена краткая характеристика ЦФС «Фотомод» и технология построения блочной сети фототриангуляции на ЦФС «Фотомод».
В третьем разделе будет подробно рассмотрено построение блочной сети фототриангуляции на ЦФС «Фотомод», включающее оценку фотографического и фотограмметрического качества исходных материалов, составление рабочего проекта, подготовку исходных данных для построения сети, внутреннее ориентирование снимков, измерение плоских координат опорных, межмаршруных и связующих точек снимков, построение и уравнивание блочной сети фототриангуляции, оценку точности, контроль качества и анализ результатов цифровой фототриангуляции.
В четвертом разделе будут приведены результаты исследования точности построения блочной сети фототриангуляции и проведён анализ результатов.
1.Цифровая фототриангуляция
1.1 Сущность, классификация и назначение фототриангуляции
Сущность фототриангуляции заключается в построении модели местности по снимках, принадлежащим одному или нескольким маршрутам, и внешнем ориентировании этой модели. Фототриангуляция позволяет определять по снимкам плановое положение и высоты опорных точек, необходимых для создания фотопланов, ортофотопланов, карт, цифровой модели рельефа (ЦМР), цифровой модели местности (ЦММ). Также позволяет определять элементы внешнего ориентирования снимков. Основная цель пространственной фототриангуляции (ПФТ) – максимально сократить трудоёмкие полевые геодезические работы, заменить их на камеральные.
ПФТ можно классифицировать[6]:
1) по количеству маршрутов:
- одномаршрутная, которая строится по снимкам, принадлежащим одному маршруту;
- многомаршрутная, или блочная, которая строится по снимкам, принадлежащим двум и более маршрутам;
2) по технологии построения сети фототриангуляции:
- аналоговая, основанная на использование универсальных приборов;
- аналитическая,основанная на применении высокоточных автоматизированных стереокомпараторов и ЭВМ;
- цифровая, при которой используются цифровые изображения;
3) в зависимости от использования физических измерений:
- с использованием физических измерений;
- без использования физических измерений;
4) по назначению:
- каркасная, развивающаяся перпендикулярно к направлению заполняющих маршрутов с целью обеспечения опорными точками, необходимыми для фототриангуляции по заполняющим маршрутам;
- заполняющая, обеспечивающая опорными точками каждую стереопару.
Различают 3 способа одномаршрутной ПФТ:
1) метод независимых моделей;
2) метод частично зависимых моделей;
3) метод связок.
Различают 3 способа многомаршрутной ПФТ:
1) способ связок;
2) способ независимых моделей;
3) способ независимых маршрутов.
1.2 Достоинства цифровой фототриангуляции
Цифровая фототриангуляция имеет следующие достоинства[6]:
1) высокая степень автоматизации;
2) высокая точность благодаря:
- возможности учёта геометрических искажений в координатах точек снимков;
- возможности обработки избыточных измерений;
- использованию мощных компьютеров;
- использованию строгих алгоритмов обработки снимков;
3) возможность обработки снимков различного формата с различными элементами внутреннего и внешнего ориентирования снимков, снимков, полученных различными съемочными системами;
4) широкие функциональные возможности;
5) решена проблема старения материала;
6) возможность улучшения изобразительного качества снимков;
7) высокая производительность труда и культура производства;
8) нет необходимости в сложном обслуживании.
1.3 Сущность основных методов цифровой и аналитической фототриангуляции
1.3.1 Маршрутная фототриангуляция методом независимых моделей
Основные этапы построения ПФТ методом независимых моделей[2]:
1) предварительная обработка результатов измерений координат точек снимков. Осуществляется переход от отсчётов, полученных при измерении снимков на приборе, к плоским координатам точек снимков x, y и учет всех систематических ошибок в координатах точек снимков (за дисторсию объектива АФА, деформацию фотоматериала, рефракцию световых лучей и др.);
2) взаимное ориентирование снимков.
На
данном этапе определяются элементы взаимного ориентирования снимков в
базисной
системе
(
).
В качестве исходного уравнения используется условие компланарности соответствующих лучей в базисной системе:
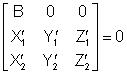, (1.1)
где
-
пространственные координаты точек левого и правого снимков. В уравнении (1.1)
известными будут 
, неизвестными
являются элементы взаимного ориентирования 
.
, (1.2)
где 
- плоские координаты
точек снимков;
- направляющие косинусы,
являющиеся функциями элементов взаимного ориентирования снимков;
- элементы внутреннего
ориентирования снимков.
На основе (1.1) получим уравнение вида
(1.3)
Уравнение (1.3) не линейны по отношению к элементам взаимного ориентирования снимков. Их решают итерационным методом, предварирительно приведя их к линейному виду разложением в ряд Тейлора, ограничиваясь производными первого порядка малости;
3) определение фотограмметрических координат точек одиночных моделей. Выполняется по формулам прямой фотограмметрической засечки:
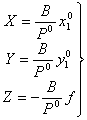(1.4)
, (1.5)
где
–
трансформированные координаты точек левого снимка,
– трансформированный
продольный параллакс.
. (1.6)
. (1.7)
4) подсоединение независимых моделей.
На данном этапе перевычисляются координаты точек в единую систему координат всей сети. Обычно в качестве системы координат маршрутной сети принимают фотограмметрическую систему координат первой модели маршрута. Для подсоединения моделей используются координаты связующих точек.
В качестве исходного принимается уравнение связи координат точек последующей модели с предыдущей:
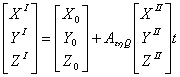, (1.8)
где
-
координаты точек в системе координат маршрутной модели (сети); 
-
координаты
этих же точек в системе координат последующей модели;
-
матрица направляющих косинусов, вычисленных через углы 
;
t -масштабный коэффициент;
-
координаты начала системы координат последующей модели в системе координат
маршрутной сети.
Этап
подсоединения модели состоит из двух процессов. Сначала вычисляются
, а
известными будут 
.
Затем
вычисляются координаты точек присоединяемой модели в системе координат
маршрутной сети. Известными будут 
и
координаты 
точек модели,
полученные по формулам (1.4).
По
формулам
(1.9)
вычисляются
координаты 
присоединяемой
модели в системе координат маршрутной сети.
5) внешнее ориентирование сети.
На данном этапе перевычисляются координаты точек сети в заданную внешнюю систему координат. Необходимо минимум три опорных точки.
Для внешнего ориентирования сети используются координаты X, Y, Z опорных точек и уравнения вида:
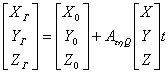. (1.9)
где 
координаты начала системы координат сети;
фотограмметрические координаты точек
сети;
геодезические координаты точек
местности.
В
начале известны координаты опорных точек в геодезической системе и
фотограмметрические координаты этих точек, полученные из уравнивания сети. В
качестве неизвестных выступают 7 элементов ориентирования геодезической сети:
.
Определив
7 этих неизвестных, будут определяться геодезические координаты 
всех
точек сети ПФТ.
6) исключение деформации сети.
Деформацию сети ПФТ можно описать различными полиномами.
Например, обобщённого типа:
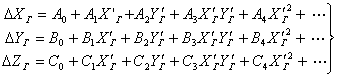, (1.10)
где
–
это коэффициенты деформации, 
– геодезические
координаты точек сети, полученные на этапе 5 из геодезически ориентированной
сети.
Из-за деформации сети после ее геодезического ориентирования на опорных точках будут получены расхождения координат :
(1.11)
Исключение
деформации сети состоит из 2 процессов: сначала будут известны
, 
опорных
точек, неизвестными будут коэффициенты 
, а
исходными для определения коэффициентов будут уравнения
(1.10).
После
определения коэффициентов деформации вычисляется величина разности
координат
характеризующие
деформацию сети для всех точек сети по формулам (1.10).
Затем вычисляются исправленные координаты точек сети:
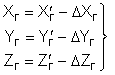. (1.12)
1.3.2 Построение блочных сетей фототриангуляции методом связок
Наиболее строгим методом построения блочных сетей пространственной фототриангуляции аналитическим и цифровым способами по сравнению с методом независимых моделей является метод связок[2]. В основе метода связок лежат уравнения коллинеарности проектирующих лучей:
,
(1.13)
В уравнении будут
известны f, x0, y0,x, y. Неизвестны
элементы внешнего ориентирования снимков 
, также X, Y, Z – координаты
точек сети ПФТ.
Уравнения (1.13) нелинейные и решаются итерационным методом.
На основе (1.13) имеем уравнение поправок вида:
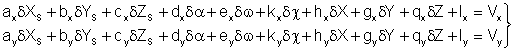, (1.14)
Уравнения (1.14) решаются по методу наименьших квадратов.
lx и ly – свободные члены, вычисляемые по формулам:
, (1.15) где 
– вычисляются по формулам
(1.13) подстановкой в них
приближённых значений
неизвестных 
.
Достоинством метода связок является то, что сеть строится и уравнивается одновременно для всех точек, входящих в блок, а также поправки находятся непосредственно к измеренным величинам, что обеспечивает более высокую точность построения сети. Недостатками этого метода являются: сложность задания приближённых значений неизвестных (для решения этой проблемы можно предварительно уровнять сеть менее строгим методом, а её результаты использовать в качестве приближённых значений), должны отсутствовать грубые ошибки, должны быть исключены систематические ошибки (или сведены к минимуму).
1.3.3 Построение блочной сети фототриангуляции объединением одиночных моделей
Этот метод основан на том[2], что сначала по каждой стереопаре, входящей в блок, строятся независимые одиночные модели, каждая из которых имеет свой масштаб и свою систему координат.
В процессе уравнивания моделей в блоке, все независимые модели приводятся к определенному масштабу и в единую пространственную систему координат на основе совместного внешнего ориентирования моделей.
Исходным является уравнение:
, (1.16)
где i – номер модели, 
- элементы внешнего ориентирования для каждой модели.
Исходными данными для формирования блока из независимых моделей служат 
, 
и 
. Используются условия равенства 0:
-
разностей 
координат опорных точек, полученных из
фототриангуляции и из полевых геодезических работ:
-
уклонений 
координат центров проектирования, полученных из ПФТ и
зафиксированных в полете с помощью бортовых приборов;
-
расхождений 
координат связующих и общемаршрутных точек, лежащих в
зоне поперечного перекрытия снимков соседних маршрутов.
Эти уравнения будут составляться для опорных точек и центров фотографирования.
Для связующих точек, расположенных в зоне тройного продольного перекрытия снимков и общемаршрутных точек, расположенных в зоне поперечного перекрытия снимков будут составляться уравнения вида:
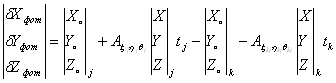(1.17)
Уравнения (1.16) и (1.17)
решаются совместно. В результате решения определяются: 
, по которым далее по формулам (1.16) определяются
координаты X, Y, Z в системе
координат блочной сети.
Достоинством этого метода является то, что он проще в реализации, а недостатком – он менее строг с точки зрения уравнивания, чем метод связок.
1.3.4 Построение блочной сети фототриангуляции объединением независимых маршрутных моделей
Сущность данного метод заключается в том[2], что объединяются независимые маршрутные сети (построенные допустим методом независимых и частично зависимых моделей). Маршрутные сети предварительно внешне ориентированы в единой пространственной прямоугольной системе координат блока. В основе объединения маршрутных сетей в единый фототриангуляционный блок используется равенство нулю: 1) разности геодезических координат полученных из геодезии и ПФТ δгеод; 2) уклонений координат центров фотографирования, полученных из фототриангуляции и зафиксированных в полёте с помощью бортовых приборов δборт;
3) расхождений координат общемаршрутных точек δфот.
Исходными
данными для объединения маршрутных сетей в единый блок служат 
, 
и 
.
Уравнивание маршрутных сетей в блоке выполняется одновременно с исключением деформации сетей ПФТ.
, (1.18)
где i – номер маршрутной модели,
Ci – коэффициенты, характеризующие деформацию фототриангуляционной маршрутной сети.
, (1.19)
где Ri – систематическая погрешность показаний бортовых навигационных приборов;
(1.20)
Уравнения (1.19) – (1.20) решаются совместно, из которых определяются неизвестные Ci и Ri.
На втором этапе для всех точек маршрутных сетей вычисляются велечины поправок
(1.21)
Вид
функции (1.21) определяется типом выбранных для уравнивания полиномов
.После
вычисления 
можно найти
исправленные координаты точек сети:
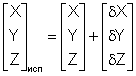(1.22)
Достоинством данного метода является то, что он проще в реализации, легче выявлять грубые ошибки в координатах общемаршрутных точек, а также результаты ПФТ по данному методу можно использовать в качестве приближённых значений неизвестных. Недостаток жёсткие требования к расположению опорных точек и их числу, также уравниваются функции от измеренных величин, а не сами измеряемые величины.
1.4 Особенности цифровой фототриангуляции
Пирамиды изображений для хранения цифровых изображений.
При обработке цифровых изображений[7] при ПФТ часто возникает необходимость просмотра снимков в уменьшенном масштабе. Для этих целей в программах ПФТ посчитанные один раз изображения уменьшенного масштаба, записываются и хранятся на диске во время всего сеанса обработки в виде «пирамид изображений». В этом случае информационное поле описывается упорядоченным набором изображений, располагаемых одно над другим.
Для формирования пирамиды изображений исходный цифровой снимок разбивается на блоки (обычно 2 х 2 пикселя). Для каждого блока вычисляется среднее арифметическое значение яркости, которое и будет присвоено пикселю для данного блока на следующем уровне пирамиды. Эта процедура повторяется необходимое число раз. Каждое последующее изображение пирамиды будет иметь разрешение в 2 раза меньше предыдущего, а занимаемый объём памяти соответственно в 4 раза
Хранение пирамид изображений оправдано, так как увеличевает скорость обработки.
Тайловая структура организации данных цифровых изображений.
В качестве модели организации данных цифровых изображений[7] используется тайловая структура, которая заключается в следующем:
Исходное изображение делится на блоки (тайлы), размер которых фиксирован.
При необходимости обработки конкретного участка изображения осуществляется перемещение на данный адрес и считывается нужный файл. Эта организация данных позволяет быстро считывать с диска и отображать на экране отдельные участки изображения.
Реляционная модель организации данных.
Для обеспечения гибкости сбора данных и хранения результатов измерения координат точек снимков в современных программных продуктах используется реляционная модель данных[7].
| Таблица 1 «Сведения о точках сети» | Таблица 2 «Сведения о снимках» | |
| Номер точки | Идентификатор снимка | |
|
|
|
|
| Описание точки | Другие параметры |
X,Y,Z 
Элементы внешнего ориентирования снимка| Таблица 3 «Сведения о точках снимка» |
| Номер точки |
| Идентификатор снимка |
| Измеренные х,у |
| Другие параметры |
Таблица 1 служит для хранения номеров и координат опорных, контрольных и связующих точек (номера точек не должны повторяться).
Таблица 2 служит для хранения информации о снимках, используемых в обработке. В качестве данных выступают идентификатор снимка, элементы внешнего ориентирования, результаты внутреннего ориентирования снимка и т.п.
В таблице 3 хранятся непосредственно измеренные координаты точек снимков х,у. Каждому измерению х,у в этой таблице соответствует номер измеряемой точки и идентификатор снимка, на котором производилось измерение.
Такая организация данных позволяет однозначно сопоставить каждому измерению соответствующую точку местности (сети) и снимок, на котором выполнено измерение. Она позволяет хранить «бесконечное» число опорных, контрольных, связующих точек и результатов измерения их координат.
Алгоритмы автоматического отождествления соответственных точек снимков.
Ключевым алгоритмом автоматизации фотограмметрических измерений является поиск соответственных точек на паре снимков[7].
В соответствии с методами представления видеоинформации все множество алгоритмов отождествления можно разделить на три класса:
- алгоритмы площадного сопоставления (ABM), основанные на сравнении двумерных функций изображений;
- алгоритмы, базирующиеся на сопоставлении структурных описаний (FBM);
- алгоритмы, в основе которых лежит разложение функции изображения по некоторому базису.
Рассмотрим подробнее первую группу. Здесь в качестве примитивов (элементов описаний), участвующих при сопоставлении двух изображений служат пиксели. Точность этих алгоритмов составляет от 0,1 до 0,2 размера пикселя. Они чувствительны к изменению радиометрических и геометрических свойств изображения, требуют больших вычислительных затрат и характеризуются большой вероятностью грубой ошибки в областях расположения высотных объектов и плохих или повторяющихся структур. Примерами площадных алгоритмов являются алгоритм взаимной корреляции и метод наименьших квадратов. Критерием подобия для этих алгоритмов соответственно служат коэффициент взаимной корреляции и сумма квадратов разностей значений яркостей сопряженных участков изображений.
Mетод взаимной корреляции.
Суть метода заключается в вычислении функции взаимной корреляции, которую для дискретных функций можно записать в виде:
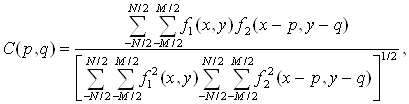(1.23)
где p и q – продольный и поперечный параллаксы на изображении f2(x, y).
M и N – соответственно ширина и высота образца или пределы, в которых определена функция f1(x,y).
Функция взаимной корреляции обладает следующими свойствами:
1)
2) если f1(x,y) и f2(x-p,y-q) независимы, то C(p, q)=0;
3)
C(p,q)=1 тогда и только тогда, когда
существует такое число b¹0, что 
.
Фактически алгоритм отыскания соответствия между функциями f1(x,y) и f2(x-p, y-q) сводится к нахождению таких p0 и q0, при которых функция C(p, q) максимальна.
Преимущество этого метода простота реализации.
К недостаткам алгоритма взаимной корреляции относятся:
- большой объем вычислений;
- алгоритм устойчиво работает только при следующих условиях: снимаемая местность плоская, взаимные углы наклона и разворота снимков не превышают 20-30°, а разномасштабность снимков менее 20-30%.
Метод наименьших квадратов
Для метода наименьших квадратов в качестве критерия подобия служит функция суммы квадратов разностей между яркостями пикселей двух изображений.
Пусть на ограниченном участке (x'[-M/2, M/2], y'[-N/2, N/2]) между функциями f1 и f2 существует зависимость:
(1.24)
Для определения искомых величин p0 и q0 составим функцию:
(1.25)
Данную функцию решаем под условием минимума:
, (1.26)
Если известны
приближенные значения неизвестных параметров (
), то раскладывая функцию(1.25) в ряд Тейлора и
ограничиваясь величинами первого порядка малости получаем линейное уравнение
относительно неизвестных Dp0 и Dq0:
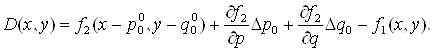(1.27)
В результате приходим к системе уравнений поправок:
(1.28)
где A – матрица коэффициентов уравнений поправок;
dX – вектор-столбец поправок к приближенным значениям неизвестных (Dp0 и Dq0);
V – вектор невязок уравнений, который характеризует величины шумовых составляющих.
От системы уравнений поправок переходим к системе нормальных уравнений:
(1.29)
где 
и 
.
После определения Dp0 и Dq0 уточняют значения искомых параметров p0 и q0 и затем выполняют следующую итерацию. Этот процесс повторяется до получения требуемой точности вычисления неизвестных.
Алгоритм наименьших квадратов по сравнению с методом взаимной корреляции обладает рядом следующих преимуществ.
Во-первых, метод наименьших квадратов позволяет оценить точность определения искомых параметров. Для оценки точности используют среднюю квадратическую ошибку (СКО) единицы веса, которая будет характеризовать влияние шумовых составляющих и качество образца, и СКО определения параметров p0 и q0, характеризующие точность отождествления соответственно по осям x и y. Значение СКО единицы веса определяется по известной формуле:
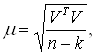(1.30)
где n – количество уравнений поправок, а k – количество неизвестных.
СКО определения неизвестных p0 и q0 выражаются формулами:
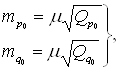(1.31)
где 
и 
– соответствующие диагональные элементы обратной матрицы
нормальных уравнений.
Во-вторых, метод наименьших квадратов позволяет вести не глобальный поиск соответственной точки, подставляя все возможные значения p и q, как в методе взаимной корреляции, а вдоль направления градиента функции.
В-третьих, как показывает практика, из всех разработанных алгоритмов отождествления метод наименьших квадратов дает наилучшие результаты в отношении точности.
В-четвертых, геометрические ограничения, накладываемые на положение и ориентацию снимков относительно плоскости объектов, несколько ослаблены при использовании метода наименьших квадратов по сравнению с методом взаимной корреляции.
К недостаткам метода наименьших квадратов следует отнести:
- алгоритм, как и все методы площадного отождествления, устойчиво работает только при незначительной разномасштабности и взаимных углах наклона и разворота снимков;
- для получения корректного решения требуется достаточно точно задать параметры p0 и q0.
Широкое распространение на практике получили следующие программные продукты цифровой фототриангуляции:
1) Softplotter фирмы Vision;
2) DPW фирмы Leica;
3) Imagine Station фирмы Intergraph;
4) Match AT – первая программа полностью автоматической ПФТ;
5) Helava Automated Triangulation System;
6) Phodis AT.
Среди российских ЦФС, в которых реализована программа цифровой ПФТ, распространение получили:
1) ЦФС Photomod фирмы Ракурс;
2) Talka, разработанная институтом проблем управления РАН;
3) ЦНИИГАиК.
Они имеют различные алгоритмы и способы реализации, высокую скорость обработки данных, удобный пользовательский интерфейс, гибкость и универсальность, возможность интерактивного режима работы оператора на всех этапах технологических процессов построения сети. По уровню автоматизации все программы ЦФТ делятся на: автоматические и полуавтоматические.
Основными технологическими процессами, которые существуют в любой программе цифровой фототриангуляции [7] являются:
1) создание проекта;
2) внутреннее ориентирование снимков;
3) измерение координат точек снимков;
4) предварительное построение сети;
5) уравнивание сети;
6) оценка точности построения сети.
2. Технология построения блочной сети фототриангуляции на ЦФС «Фотомод»
2.1 Краткая характеристика ЦФС «Фотомод»
Цифровая фотограмметрическая система PHOTOMOD предназначена для решения полного комплекса задач от создания блока изображения до построения моделей рельефа, создания цифровых карт местности и ортофотопланов. Система PHOTOMOD включает средства обработки аэрофотоснимков и сканерных изображений, полученных с помощью различных сенсоров таких, например, как IKONOS, QuickBird, SPOT, ASTER или IRS.
Система PHOTOMOD производится российской компанией Ракурс (Москва) и динамично развивается, начиная с версии 1.1, выпущенной в 1994 году.
Система цифровой фотограмметрии PHOTOMOD включает следующие основные модули[5]:
- PHOTOMOD Montage Desktop – создание и управление проектами
- PHOTOMOD AT – сбор данных и измерения при обработке блока изображений
- PHOTOMOD Solver – уравнивание сети фототриангуляции
- PHOTOMOD StereoDraw – 3D векторизация в стереорежиме по стереопаре
- PHOTOMOD StereoVectOr – параллельная работа с картой формата PHOTOMOD VectOr в окнах StereoDraw (3D векторизация) и VectOr (векторизация по ортофото и редактирование карты)
- PHOTOMOD DTM – построение моделей рельефа, горизонталей по стереопаре
- PHOTOMOD Mosaic – построение ортофотопланов
- PHOTOMOD VectOr – создание и вывод на печать цифровых карт
- PHOTOMOD ScanCorrect – исправление искажений, вносимых в исходные изображения при использовании планшетных сканеров
2.2 Основные процессы технологии построения блочной сети фототриангуляции на ЦФС «Фотомод»
Структурой данных системы PHOTOMOD является[5] проект, который содержит все необходимые файлы для работы – изображения, модели рельефа, трёхмерные векторные объекты, таблицы баз данных модуля PHOTOMOD AT и многое другое. В терминологии системы PHOTOMOD эти файлы называются ресурсами. Каждый ресурс имеет идентификатор, который однозначно указывает на него во всей системе. Идентификатор – это строка специального формата не изменяемая пользователем. У каждого ресурса есть имя, задаваемое пользователем. В отличие от идентификатора, имя может совпадать у нескольких ресурсов или вообще отсутствовать. Также система хранит для каждого ресурса его размер, даты создания и последнюю модификацию, а также тип и подтип.
Ресурсы хранятся в созданных при настройке конфигурации системы хранилищах, которые могут быть расположены на различных локальных машинах. Хранилище представляет собой каталог на диске, где в виде файлов лежат данные ресурсов.
Хранилище может быть локальным, если оно расположено на диске данного компьютера или удалённым, если оно доступно через сеть Microsoft Windows.
Для создания хранилища ресурсов нажимают кнопку “добавить хранилище” в Панели управления PHOTOMOD.
Система PHOTOMOD производит обработку проекта в 4 этапа: формирование сети, измерение сети, уравнивание сети, обработка сети.
На этапе формирования сети производится ввод маршрутов и изображений блока. При необходимости изображения могут быть развёрнуты или переставлены в пределах маршрута. В данном случае использовались снимки масштаба 1:12000. Для удобной работы на этапе формирования блока используется окно “Схема блока”. Для формирования блока используются следующие операции: добавить маршрут, удалить маршрут, перемещение маршрута «вверх» по схеме, перемещение маршрута «вниз» по схеме, поворот/отражение всех изображений маршрута, переставить снимки маршрута в обратном порядке, добавить изображение, удалить изображение, переместить изображение «влево», переместить изображение «вправо».
Для перехода на этап “Измерение сети” необходимо нажать зелёную стрелку в левой части панели” Формирование сети” окна Диспетчер проекта. На этапе “Измерение сети” запускается модуль PHOTOMOD AT, в котором происходит подготовка данных для уравнивания сети фототриангуляции. Обработка проекта в модуле PHOTOMOD AT включает внутреннее ориентирование, измерение координат х, у опорных точек, измерение межмаршрутных связей и взаимное ориентирование.
Внутреннее ориентирование выполняется для вычисления значений параметров, определяющих положение и ориентацию системы координат снимка относительно системы координат исходного цифрового изображения. Кроме того, при внутреннем ориентировании могут быть определены параметры, описывающие систематическую деформацию снимка. Значения параметров, определённых в результате выполнения внутреннего ориентирования, используются для преобразования измерений из системы координат исходного цифрового изображения в систему координат снимка.
При внутреннем ориентировании измеряются координатные метки. Измерения можно проводить в ручном, полуавтоматическом или автоматическом режиме.
Автоматическое внутреннее ориентирование заключается в поиске аналогичных объектов – координатных меток на всех снимках блока. Выбранная Область поиска должна быть достаточно велика для случаев неравномерной нарезки снимков (когда соответствующие координатные метки на разных снимках находятся на разном расстоянии от края изображения). Область метки должна захватывать изображение метки полностью. Области метки и поиска отображаются прямоугольниками как в основном окне с изображением диалога Внутреннее ориентирование, так и в окне-«линзе». Изображение, для которого внутреннее ориентирование было выполнено вручную, является эталоном.
После измерения координат меток производится внутреннее ориентирование по одному, из вариантов преобразования:
- поворот, масштаб, сдвиг;
- аффинное;
- проективное.
Внешнее ориентирование и исключение деформации сети триангуляции осуществляется с помощью измерения координат опорных точек.
Для построения сети пространственной фототриангуляции на стереопарах, помимо координат опорных точек, необходимо измерить связующие точки, служащие для построения моделей по стереопарам смежных снимков маршрута для объединения их в маршрутные и блочные сети.
Измерение новых связующих точек и точек сгущения может выполняться 3-мя способами:
- добавление точек с помощью коррелятора;
- добавление точек без коррелятора;
- автоматическое добавление точек.
Для перехода на этап “Уравнивание сети” нажмите зелёную стрелку в левой части панели” Измерение сети” окна Диспетчер проекта. На этапе “Уравнивание сети” запускается модуль PHOTOMOD Solver, в котором происходит уравнивание блочной сети фототриангуляции. После выполнения уравнивания блок изображений отображается в 2D окне PHOTOMOD Montage Desktop в соответствии с выбранной системой координат, а в окне Схемы блока помимо маршрутов и изображений отображаются имена стереопар.
На основании поставленных задач при обработке используются модули: PHOTOMOD DTM, PHOTOMOD StereoDraw – 3D, PHOTOMOD StereoVectOr, PHOTOMOD Mosaic, PHOTOMOD VectOr. В ЦФС «Фотомод» для построения сети применяются два способа метод построения блочной сети объединением независимых моделей и объединением независимых маршрутных моделей. Результатами ПФТ являются: элементы внешнего ориентирования снимков, либо координаты точек местности, которые в последствии будут использованы как опорные.
3. Построение блочной сети фототриангуляции на ЦФС «Фотомод»
3.1 Оценка фотографического и фотограмметрического качества исходных фотоматериалов
Была произведена визуальная оценка фотографического качества. На снимках заэкспонирована сельская равнинная местность. При аэрофотографировании использовалась чёрно-белая панхроматическая аэропленка. Полученные снимки были сканированы в цифровой вид с разрешением 14 мкм. В работе использовано 8 снимков, принадлежащих двум маршрутам, по 4 снимка в каждом. На каждый снимок впечатано по 8 координатных меток. Использованные снимки удовлетворительного качества. Царапины и пятна наблюдаются в незначительном количестве. Дефекты аэронегативов, а также изображения облаков, производственных дымов и теней от них, блики, ореолы не мешают выполнению фотограмметрических работ и дешифрированию аэрофотоснимков. Сканированные снимки имеют резкое и средне проработанное изображение почти по всему полю в светах и тенях. К краям снимков резкость значительно падает. Обеспечена хорошая читаемость основных контуров местности и номера аэрофотоснимков.
Оценка фотограмметрического качества исходных материалов осуществляется следующим образом.
Технические средства аэрофотосъемки обеспечивают возможность получения черно-белых аэронегативов с минимальным линейным смазом фотоизображения, не превышающим 0,05 мм для масштабов 1:10000 и мельче. Средний масштаб используемых снимков – 1:12000, разномасштабность снимков можно определить как[4] :
*100% = 2% ,
(3.1)
Разномасштабность снимков составила 2%, что удовлетворяет допуску в 3%.
Высота фотографирования (высота полета над средней плоскостью участка) определяется по формуле:
H = f*m , (3.2)
где f – фокусное расстояние АФА (f=303,346 мм);
m – знаменатель масштаба фотографирования.
H =3640м
Максимальное превышение в пределах съемочного участка 83,829 м.
=0,02 ,
(3.3)
где h – максимальное превышение точек местности над средней плоскостью съёмочного участка;
H – высота полета над средней плоскостью участка;
δτh – смещение точек вызванное рельефом местности.
В соответствии с эти
критерием продольное перекрытие снимков не должно выходить за пределы интервала
от 56% до 66%. При выполнении измерений получено среднее продольное перекрытие
снимков 
=
64% , что удовлетворяет допуску.
Поперечное перекрытие
смежных маршрутов для масштабов аэрофотосъемки 1:25000 - 1:10000 составляет 
= от 20% до
35%.Данные снимки имеют 
=22%, достаточное
для проведения фотограмметрических работ с этими материалами.
Углы наклона
аэрофотоснимков, полученных стабилизированными аэрофотоаппаратами, не превышают
2
, допуск
не более 2۫ . На съемочном участке количество
максимальных значений взаимных продольных углов наклона не превышает 2,5%
стереопар (допуск – 3%), а количество взаимных поперечных углов наклона – около
5% стереопар.
Непараллельность базиса
фотографирования (“ёлочка”) не должна превышать 12
для фокусного расстояния 303,345 мм (при котором были получены обрабатываемые снимки). Ввиду отсутствия контактных отпечатков
величина ёлочки не определялась.
Можно сделать вывод что с данным материалам можно проводить пространственную фототриангуляцию.
3.2 Составление рабочего проекта построения блочной сети ПФТ
Составление рабочего проекта - это выбор и разметка на аэрофотоснимках точек, необходимых для построения сети ПФТ с целью ее дальнейшего использования.
Исходными материалами для проектирования служат[1]:
-снимки с наколотыми и оформленными опорными точками и с абрисами, показывающими расположение этих точек относительно контуров;
-эти же снимки в цифровом виде;
-паспорт аэрофотосъемки;
-каталог координат опорных точек.
В проект включают[2]:
- опорные точки, с помощью которых осуществляется внешнее ориентирование и исключение деформации сети фототриангуляции;
- контрольные точки (планово-высотные, плановые или высотные опознаки), необходимые для выполнения оценки точности фототриангулирования;
- связующе точки, предназначенные для объединения элементарных звеньев в маршрутную модель;
- определяемые фотограмметрические точки, координаты которых необходимы для последующего решения задач по аэрофотоснимкам, определяется заказчиком;
- межмаршрутные точки,предназначенные для связи маршрутов в единый блок.
Опорные точки наносятся со снимков полевой подготовки. Минимальное их количество для маршрута ограниченной длины равно пяти. В работе было использовано 9 опорных точек.
Связующие точки выбираются в зоне тройного продольного перекрытия снимков на максимальном расстоянии от главных точек, Минимальное число связующих точек равно трем.
Таблица 3.1- Каталог координат опорных точек
| Порядковый номер | Название опорной точки | X(м) | Y(м) | Z(м) |
| 1 | 2844-1 | 5886,200 | 5498,070 | 125,300 |
| 2 | 2844-2 | 4885,030 | 5558,800 | 140,890 |
| 3 | 2844-3 | 3790,500 | 5378,650 | 170,080 |
| 4 | 2844-4 | 5563,710 | 6318,440 | 134,450 |
| 5 | 2845-1 | 5143,160 | 3976,670 | 147,100 |
| 6 | 2845-2 | 3930,880 | 3644,100 | 185,410 |
| 7 | 2845-3 | 2781,550 | 5186,160 | 209,220 |
| 8 | 2850-1 | 2937.040 | 6405,300 | 189,480 |
| 9 | 2850-2 | 4527,190 | 7084,690 | 154,820 |
Схема размещения опорных точек
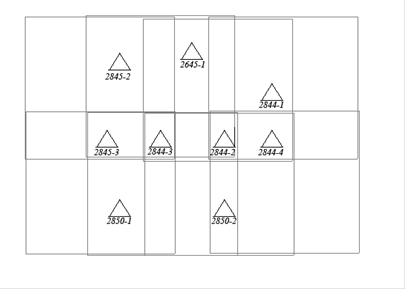
3.3 Подготовка исходных данных для построения сети и ввод параметров проекта
В качестве исходных данных для построения сети[1] являются:
- масштаб снимков;
- паспортные данные камеры;
- снимки с опознаками;
- снимки в цифровом виде;
- координаты опорных точек.
При создании проекта выбирается внешняя система координат. В данном случае системой координат является декартова левая. Масштаб снимков составляет 1:12000.
Паспортные данные камеры вводятся на этапе внутреннего ориентирования снимков в редакторе камер[5]:
- камера - RC 30 №17136;
- дата калибровки;
- единицы измерения - мм
- фокусное расстояние – 303,346 мм;
- координаты главной точки
= 0,00075 мм, 
= 0,000875 мм;
- координаты координатных меток.
Таблица 3.2-Координаты координатных меток
| № | х(мм) | у(мм) |
| 1 | 106,000 | -105,998 |
| 2 | -105,998 | -105,998 |
| 3 | -105,999 | -105,997 |
| 4 | 106,000 | 106,000 |
| 5 | -0,001 | -111,995 |
| 6 | -111,997 | 0,000 |
| 7 | 0,003 | 112,000 |
| 8 | 111,998 | 0,001 |
Информация о дисторсии.
Дисторсия «4 направления “x”»
Точка симметрии x = -0,017 мм; y = -0,022 мм.
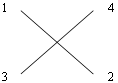
Рисунок 3.1-Четыре направления измерения дисторсии по оси x
Таблица 3.3-Информация о дисторсии
| R | 1(направление)мм | 2(направление)мм | 3(направление)мм | 4(направление)мм |
| 10 | -0,0003 | -0,0012 | 0,0000 | -0,0012 |
| 20 | -0,0014 | -0,0029 | -0,0007 | -0,0020 |
| 30 | -0,0030 | -,0031 | -0,0009 | -0,0021 |
| 40 | -0,0026 | -0,0032 | -0,0004 | -0,0015 |
| 50 | -0,0019 | -0,0021 | -0,0005 | -0,0011 |
| 60 | -0,0021 | -0,0013 | 0,0003 | -0,0004 |
| 70 | -0,0010 | -0,0011 | 0,0001 | -0,0003 |
| 80 | -0,0014 | -0,0004 | 0,0005 | 0,0002 |
| 90 | -0,0005 | -0,0005 | 0,0004 | -0,0002 |
| 100 | -0,0011 | -0,0004 | 0,0004 | -0,0007 |
| 110 | ||||
| 120 | 0,0007 | -0,0003 | 0,0001 | -0,0011 |
| 130 | 0,0008 | 0,0011 | -0,0002 | 0,0015 |
| 140 | 0,0001 | 0,0011 | 0,0001 | 0,0010 |
| 148 | 0,0037 | 0,0033 | 0,0016 | 0,0034 |
По окончанию ввода исходных данных можно приступать к процессу внутреннего ориентирования снимков.
3.4 Внутреннее ориентирование снимков
Окно “Внутреннее ориентирование” показывает два списка “Изображения” и “Камеры”. Список “Изображения” содержит имена снимков и маршрутов, к которым они принадлежат, с указанием состояния: ориентирован да или нет снимок. В списке “Камеры” показан список камер, используемых в текущем проекте, которые могут быть добавлены в проект из каталога камер.
При внутреннем ориентировании снимков измеряются координаты координатных меток. Измерения можно проводить вручную, либо автоматически. Для измерения координат координатных меток следует выбрать измеряемую метку в таблице меток, затем выполнить точное позиционирование маркера на выбранную метку. После измерения 2-х новых меток при выборе третьей и последующих меток в списке происходит автоматическое позиционирование маркера в окрестности текущей метки, в последствии оператор вручную точно позиционирует маркер в центр координатной метки. Внутреннее ориентирование снимков выполнялось в ручном режиме.
Перед запуском процедуры автоматического внутреннего ориентирования снимков необходимо выполнить внутреннее ориентирование хотя бы для одного изображения вручную. Автоматическое внутреннее ориентирование заключается в поиске аналогичных объектов – координатных меток на всех снимках блока. Выбранная область поиска должна быть достаточно велика для случаев неравномерной нарезки снимков. Область метки должна захватывать ее изображение полностью. Области метки и поиска отображаются прямоугольниками как в основном окне с изображением диалога «Внутреннее ориентирование», так и в окне-«линза». Изображение, для которого внутреннее ориентирование было выполнено вручную, является эталоном.
После измерения координат меток необходимо произвести внутреннее ориентирование снимков, выбрать один из вариантов преобразования:
- поворот, масштаб, сдвиг;
- аффинное;
- проективное.
В работе было использовано аффинное преобразование.
Аффинные преобразования [5]выполняются по формулам:
x = ао + а1 xц + а2 yц
y = bo + b1 xц +b2 yц (3.4)
где ai, bi - параметры аффинного преобразования;
x, y – плоские координаты точек снимка;
xц, yц - плоские координаты точек цифрового изображения.
3.5 Измерение плоских координат опорных, межмаршрутных и связующих точек снимков, включенных в проект
Работа с опорными точками в модуле PHOTOMOD AT[5] проходит в два этапа.
Первый этап ввод геодезических координат опорных точек. Для каждой точки вводятся имя опорной точки, её X, Y, Z координаты и значения весов по каждой координате. Поле «Тип» используется для выбора типа той или иной точки – опорная или контрольная. Контрольные точки не участвуют в уравнивании сети фототриангуляции, а используются для оценки точности. В работе использовано 9 опорных точек.
Дальше производим измерения координат опорных точек на снимках. Чтобы измерить координаты опорной точки на снимке, необходимо выбрать нужный снимок из списка и нажать на кнопку “Измерить точку”. Появляется окно “Измерение опорных точек с растровым изображением выбранного снимка”. Опорные точки должны быть точно опознаны и их координаты измерены только на одном из снимков. На других снимках координаты опорной точки измеряются при выполнении этапов “Межмаршрутные связи” и “Измерение точек сети”. Для достижения нужной точности необходимо, чтобы опорные точки равномерно располагались по блоку.
Для построения сети пространственной фототриангуляции на стереопарах, помимо опорных точек, необходимо измерить координаты связующих точек, служащие для построения моделей по стереопарам смежных снимков маршрута для объединения их в маршрутные сети и координаты межмаршрутных точек для объеденения их в блочные сети.
Если фототриангуляция выполняется для определения координат и высот точек, используемых как опорные при последующей фотограмметрической обработке одиночных снимков и стереопар, эти точки необходимо выбирать на изображениях чётких контуров местности.
Второй этап “Измерение координат опорных точек на изображениях”. Под измерением координат точек понимается их стереоскопическое измерение, т.е. измерение координат одновременно на двух снимках стереопары.
При построении блочной сети фототриангуляции межмаршрутные точки, служащие для объединения стереопар в блок, должны быть расположены в зонах поперечного перекрытия снимков.
Межмаршрутные и связующие точки должны быть перенесены в каждом маршруте хотя бы на один соседний снимок, иначе они не будут участвовать в процессе уравнивания.
Измерение координат межмаршрутных точек осуществляется на вкладке “Межмаршрутные связи”. Вкладка содержит два списка изображений: «Маршрут 1» и «Маршрут 2». Для ввода связующих точек выбирают два снимка соседних маршрутов, указав сначала маршруты, которым они принадлежат, а затем – сами снимки. Для осуществления межмаршрутных связей необходимо минимум 2 связующих точки на каждом снимке.Также имеется возможность добавить межмаршрутные точки между маршрутами в автоматическом режиме.
Измерение координат связующих точек заключается в определении их положения на соседних снимках блока. Измерение координат связующих точек в пределах стереопары одного маршрута осуществляется на вкладе “Измерение точек сети”, содержащей окно списка маршрутов и окно списка стереопар текущего маршрута. Знак плюс или минус показывает, производились или нет измерения точек на данной стереопаре. Для выполнения измерений координат точек сети необходимо выбрать маршрут из списка маршрутов, затем одну из стереопар выбранного маршрута и нажать кнопку “Выполнить ориентирование”.
Если на одном из снимков стереопары измерены координаты опорных или межмаршрутных точек, то измерения рекомендуется начинать с них.
Измерение координат новых связующих точек и точек сгущения может выполняться 3-мя способами:
- добавление точек с помощью коррелятора;
- добавление точек без коррелятора;
- автоматическое добавление точек.
При возникновении необходимости измерения координат опорных/контрольных и связующих точек в стереорежиме (если точки расположены на вертикально стоящих объектах, на объектах видимых в монорежиме только на одном из изображений стереопары). Измерения производятся с помощью стереолинзы (работа в стереолинзе с подвижным стереомаркером) или в режиме стереокомпаратора (работа с неподвижным маркером и подвижными изображениями).
Координаты связующих точек должны быть измерены в шести стандартных зонах, минимум необходимо 5 точек, 6-ая точка в шестой стандартной зоне – контрольная. Для большей точности проводились измерения трех точек в каждой стандартной зоне.
3.6 Построение и уравнивание блочной сети фототриангуляции
Построение и уравнивание блочных сетей фототриангуляции[5] производится в модуле PHOTOMOD Solver. Предварительно необходимо задать основные параметры в окне “параметры”. Систему координат выбираем декартову левую. На вкладке “Уравнивание” можно выбрать метод уравнивания (независимых маршрутов или независимых моделей). В работе использовался метод независимых моделей, так как он более точен. Построение свободной модели используется в случае отсутствия опорных точек на момент уравнивания блока. В отчет включаем ошибки уравнивания по стереопарам, по снимкам, допуски на них, элементы внешнего ориентирования снимков, каталог координат точек блока, устанавливаем масштаб съёмки 1:12000, указываем допустимые ошибки по X, Y, Z.
Измерение координат связующих точек заключается в определении их положения на соседних снимках блока. Несходимость координат связующих точек может быть обусловлена ошибками взаимного ориентирования снимков, ошибками в координатах опорных точек, или неправильными параметрами уравнивания.
Метод построения блочной сети ПФТ из независимых моделей основан на том, что сначала по каждой стереопаре, входящей в блок, строятся независимые одиночные модели, то есть будут получены пространственные координаты X, Y, Z точек всех одиночных моделей, вычисленные через элементы взаимного ориентирования снимков. Каждая из этих моделей имеет свой масштаб и свою систему координат. В процессе уравнивания моделей в блоке все независимые модели приводятся к нужному масштабу и в единую пространственную систему координат на основе совместного внешнего ориентирования моделей.
Для просмотра полной статистики уравнивания нажимается кнопка “отчет”. В отчёте приводится информация по отклонениям координат на опорных, контрольных и связующих точках и центрах проекций в целом по блоку и по каждой точке, каталог координат точек, элементы внешнего ориентирования снимков. В результате ПФТ были получены элементы внешнего ориентирования снимков см. таблицу 3.4.
Таблица 3.4-Элементы внешнего ориентирования снимков
| № снимка | Xs | Ys | Zs | α | ω | |
| 2843 | 6340,731 | 5403,867 | 3850,887 | 0,8857628 | -0,6158622 | 67,7874037 |
| 2844 | 5304,585 | 4965,452 | 3854,065 | -0,5584036 | -0,1511276 | 67,7268693 |
| 2845 | 4285,126 | 4539,198 | 3855,635 | -0,1239378 | 0,0528839 | 67,8520431 |
| 2846 | 3317,966 | 4140,984 | 3852,939 | 0,5877018 | -0,2065169 | 67,9083380 |
| 2849 | 2563,822 | 5932,929 | 3861,617 | -1,3113397 | 0,0811334 | 66,8773177 |
| 2850 | 3563,444 | 6359,447 | 3859,941 | -0,3739880 | -0,1130132 | 66,5892221 |
| 2851 | 4569,063 | 6790,738 | 3862,715 | -0,2068379 | -0,2312753 | 66,6201950 |
| 2852 | 5567,391 | 7216,490 | 3861,913 | -0,1788455 | -0,4132922 | 66,6928196 |
3.7 Оценка точности, контроль качества и анализ результатов цифровой ПФТ
После построения сети ПФТ выполняется апостериорная оценка точности результатов ПФТ, которая включает:
1) вычисление максимальных и средних квадратических ошибок (СКО) характеризующих точность выполнения отдельных этапов построения сети ПФТ;
2) контроль качества результатов ПФТ;
3) анализ результатов с целью обнаружения грубых ошибок в исходных данных, либо в результатах измерения координат точек снимков.
При построении блочной сети ПФТ с использованием ЦФС «Фотомод» оценка точности результатов выполняется на следующих этапах:
- внутреннее ориентирование снимков;
- взаимное ориентирование снимков;
- подсоединение моделей;
- уравнивание моделей в блоке.
Рассмотрим этапы апостериорной оценки точности результатов ПФТ:
1) внутреннее ориентирование снимков. При выполнении данного процесса на ЦФС «Фотомод» вычисляется коэффициент К по формуле:
,
(3.5)
где 
- расстояния
между координатными метками по осям x и y на снимке.
В инструкции [3] указано, что величина коэффициента деформации отличается от 1 не более, чем на несколько единиц четвёртого после десятичной точки знака, который вычисляется по формуле:
, (3.6)
где 
- расстояние
между координатными метками из паспорта АФА.
Также в инструкции приведено, что разница коэффициентов деформации снимков по осям x и y не должна превышать несколько единиц пятого знака после десятичной точки и вычисляется как:
, (3.7)
На этапе внутреннего ориентирования снимков при работе на ЦФС «Фотомод» выдаются разности координат координатных меток Δx, Δy и СКО (mΔx, mΔy) этих разностей. Величины Δx, Δy вычисляются по формулам:
Δx = x - xпасп
Δy = y – yпасп (3.8)
где x, y – плоские координаты координатных меток в системе координат снимков;
xпасп, yпасп – плоские координаты этих меток известные из паспорта АФА.
В таблице 3.5 приведены Δxmax, Δymax – максимальные значения разностей координат координатных меток, полученные при внутреннем ориентировании снимков блока.
Величины mΔx, mΔy вычисляются по формулам:
, (3.9)
где КМ – число координатных меток.
На обрабатываемых снимках число координатных меток составляло 8.
В таблице 3.5 представлены mΔx, mΔy – максимальные из всех полученных ошибок снимков блока. Величины Δx, Δy вычисляются для каждой координатной метки снимков блока, а mΔx, mΔy для каждого снимка.
2) взаимное ориентирование снимков. Взаимное ориентирование снимков при ФТ на ЦФС «Фотомод» выполняется в базисной системе. Велечины, характеризующие точность выполнения взаимного ориентирования снимков, будут следующие:
- δq – остаточный поперечный параллакс, вычисленный в базисной системе по формуле:
, (3.10)
- mδq – СКО остаточного поперечного параллакса, которая вычисляется по формуле:
, (3.11)
где n – число точек в стереопаре.
Величина δq вычислена для каждой точки, каждой стереопары, а mδq – для каждой стереопары. В инструкции указано, что СКО остаточного поперечного параллакса не должна превышать 10мкм. В таблице 3.5 приведено максимальное значение δq и максимальная величина mδq, полученные при взаимном ориентирование снимков всех стереопар блока.
Кроме этих величин точность взаимного ориентирования снимков характеризуют:
- СКО единицы веса, вычисляемая по формуле:
,
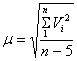(3.12)
- СКО определения элементов взаимного ориентирования, вычисленные по формулам:
, (3.13)
где Qii – диагональные элементы обратной весовой матрицы.
В данной
формуле 
,
где B – матрица коэффициентов нормальных
уравнений.
3) подсоединение одиночных моделей. Оценка точности подсоединения одиночных моделей выполняется:
- по расхождениям координат связующих точек, вычисляемым по формулам:
ΔXсв = Xk – X(k-1)
ΔYсв = Yk – Y(k-1) , (3.14)
ΔZсв = Zk – Z(k-1)
где Xk, Yk, Zk – координаты связующих точек последующей модели после перевычисления их в систему координат предыдущей модели, т.е. блока;
Xk-1, Yk-1, Zk-1 – координаты связующих точек в системе координат блока.
- по СКО разностей координат связующих точек, вычисленных по формулам:
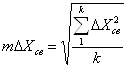
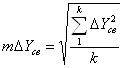, (3.15)
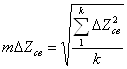
где к – число связующих точек.
Величины ΔXсв, ΔYсв, ΔZсв вычисляются для каждой связующей точки, а величины mΔXсв, mΔYсв, mΔZсв вычисляются по количеству зон тройного продольного перекрытия снимков. Максимальные значения величин ΔXсв, ΔYсв, ΔZсв, mΔXсв, mΔYсв, mΔZсв, полученных при построении сети, представлены в таблице 3.5 . В инструкции указано, что СКО координат связующих точек, вычисленные при подсоединении смежных моделей, не должны превышать: mΔXсв, mΔYсв – 15мкм, в масштабе снимков, а по высоте mΔZсв – 15мкм умноженная на отношение f/b в масштабе снимков;
- кроме того при подсоединении моделей точность подсоеденения характеризуют СКО единицы веса, вычисленная по формуле
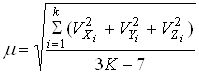, (3.16)
и СКО определения элементов подсоединения моделей
,
(3.17)
4) уравнивание сети. При уравнивании сети ПФТ в ЦФС «Фотомод» по методу независимых моделей апостериорная оценка точности результатов выполняется следующим образом:
- по разности координат связующих и межмаршрутных точек по формулам (3.14);
- по СКО разности координат связующих и межмаршрутных точек по формулам (3.15).
В инструкции указаны максимальные расхождения координат ΔX, ΔY, ΔZ общемаршрутных точек, равные 40мкм в масштабе снимков. При уравнивании сети ПФТ методом независимых моделей одновременно решаются уравнения, составленные для опорных точек, центров фотографирования, связующих и общемаршрутных точек. Поэтому координаты точек сети ПФТ в результате уравнивания будут получены в геодезической системе координат. Окончательная оценка точности сети ПФТ выполняется:
- по разностям координат опорных и контрольных точек, вычисленным по формулам:
,
(3.18)
где 
- координаты
опорных точек в геодезической системе координат вычисленные в результате ПФТ;
- координаты
опорных точек, вычисленные из полевых работ.
Разности координат контрольных точек вычисляются:
, (3.19)
где 
- координаты
контрольных точек в геодезической системе координат, вычисленные в результате
ПФТ;
- координаты
контрольных точек, вычисленные из полевых работ.
- по СКО разностей координат опорных точек
,
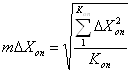
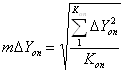(3.20)
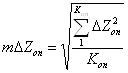
где 
- количество
опорных точек.
- по СКО разностей координат контрольных точек
,
(3.21)
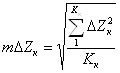
где 
- количество
контрольных точек.
Значения ΔX, ΔY, ΔZ, mΔX, mΔY, mΔZ приведены в таблице 3.3 для опорных и контрольных точек.
- по расхождению планового положения опорных и контрольных точек:
, (3.22)
, (3.23).
- по СКО расхождений планового положения опорных и контрольных точек:
, (3.24)
, (3.25).
Значения ΔL,mΔL для опорных и контрольных точек приведены в таблице 3.5.В инструкции приведены допустимые средние расхождения высот на опорных точках блочной сети
δhоп доп = 0,15* hсеч. , (3.26)
Высота сечения рельефа равна hсеч = 2,5 м, тогда средняя ошибка расхождения высот δhоп доп = 0,15*2,5 . Для определения СКО вычисления высот опорных точек, которые соответствуют требованиям инструкции, необходимо использовать коэффициент 1,25, т.е.
mΔZоп доп = 1,25* δhоп доп , (3.27)
где 1,25 – коэффициент перехода от средних к средним квадратическим ошибкам.
В инструкции приведены допустимые средние расхождения высот на контрольных точках блочной сети
δhк доп = 0,25* hсеч. , (3.28)
Высота сечения рельефа равна hсеч = 2,5 м, тогда средняя ошибка расхождения высот δhк доп = 0,15*2,5 . Для определения СКО вычисления высот опорных точек, которые соответствуют требованиям инструкций необходимо использовать коэффициент 1,25, т.е.
mΔZк доп = 1,25* δhк доп , (3.29).
Допустимые средние ошибки планового положения опорных точек не должно превышать δlоп доп = 0,2 мм , а контрольные – δlк доп = 0,3 мм в масштабе карты.
Тогда:
mΔLоп доп = 1,25* δlоп доп*M , (3.30)
mΔLк доп = 1,25* δlк доп*M , (3.31)
где М – знаменатель масштаба карты (М=2000).
В инструкции приведены предельные расхождения координат опорных и контрольных точек, не должны превышать удвоенных средних ошибок:
ΔLдоп = 2* δlдоп*M , (3.32)
ΔZдоп = 2* δh , (3.33)
Придельные расхождения координат считаются как для опорных так и для контрольных точек по формулам (3.22).
Как видно из таблицы 3.5 все величины,характеризующие точность построения сети ПФТ на ЦФС «Фотомод» удовлетворяют допускам. Значит материалы пригодны для дальнейшего использования.
Таблица 3.5 - Сводная таблица оценки точности построения блочной ПФТ.
| Этап ПФТ | Апостериорная оценка точности | Допуски по инструкции |
| 1 . Внутреннее ориентирование снимков | ||
| |kdх- 1| | ——— | Величина коэффициента деформации отличается от 1 не более, чем на несколько единиц четвёртого после десятичной точки знака |
| |kdу- 1| | ——— | |
| kdх - kdу | ——— | Разница коэффициентов деформации снимков по осям x и y не должна превышать несколько единиц пятого знака после десятичной точки |
| Δxmax , MM | 0,014 | ——— |
| Δymax , MM | 0,013 | ——— |
| mΔx , MM | 0,006 | ——— |
| mΔy , MM | 0,007 |
——— - |
| 2. Взаимное ориентирование снимков | ||
| δqmax , MM | 0,0036 | ——— |
| mδq , MM | 0,0019 | 0,01 |
| 3. Подсоединение моделей | ||
| Δxсв , MM | 0,00076 | ——— |
| Δyсв , MM | 0,0031 | ——— |
| Δzсв , MM | 0,01036 | ——— |
| mΔxсв max , MM | 0,003 | 0,015 |
| mΔyсв max , MM | 0,00152 | 0,015 |
| mΔzсв max, MM | 0,00557 | 0,046 |
| 4. Уравнивание сети ПФТ | ||
| ΔXоп , M | 0,375 | 0,8 |
| ΔYоп , M | 0,407 | 0,8 |
| ΔZоп , M | 0,598 | 0,8 |
| mΔX оп , M | 0,195 | 0,5 |
| mΔYоп , M | 0,218 | 0,5 |
| mΔZоп , M | 0,372 | 0,5 |
| ΔLГ , M | 0,257 | 0,4 |
| mΔLГ , M | 0,283 | 0,5 |
| ΔXГ оп ср, M | 0,163 | 0,4 |
| ΔYГ оп ср , M | 0,161 | 0,4 |
| ΔZГ оп ср, M | 0,343 | 0,4 |
| ΔXГ к ср, M | —— | 0,6 |
| ΔYГ к ср , M | —— | 0,6 |
| ΔZГ к ср, M | —— | 0,6 |
| mΔXГ к , M | —— | 0,75 |
| mΔYГ к , M | —— | 0,75 |
| mΔZГ к , M | —— | 0,75 |
4. Исследование точности построения блочной сети фототриангуляции с использованием ЦФС «Фотомод»
Результаты исследования точности в зависимости от способа уравнивания приведены в таблице 4.1. Как видно из таблицы метод независимых моделей даёт большую точность по сравнению с методом независимых маршрутов. Объясняется это тем, что метод независимых маршрутов предъявляет большую требовательность к расположению опорных точек и их количеству из-за того, что маршрутные сети предварительно внешне ориентируются независимо друг от друга, неизбежно возникает деформация, которая затем исключается при помощи полиномов. Метод независимых маршрутов менее строг с точки зрения МНК.
Таблица 4.1Оценка точности построения блочной ПФТ по методу независимых маршрутов и по методу независимых моделей
| Этап ПФТ | Апостериорная оценка точности | Допуски по инструкции | |
| Метод независимых маршрутов | Метод независимых моделей | ||
| ΔXоп max, M | 0,328 |
0,375 0000000 |
0,8 |
| ΔYоп max , M | 0,407 | 0,327 | 0,8 |
| ΔZоп max , M | 0,585 | 0,598 | 0,8 |
| mΔX оп, M | 0,183 |
0,195 00 |
0,5 |
| mΔYоп, M | 0,218 | 0,180 | 0,5 |
| mΔZоп, M | 0,372 | 0,357 | 0,5 |
| ΔLГ max , M | 0,257 | 0,254 | 0,4 |
| mΔLГ, M | 0,283 | 0,265 | 0,5 |
| ΔXГ оп ср, M | 0,155 |
0,163 0 |
0,4 |
| ΔYГ оп ср , M | 0,161 |
0,140 0 |
0,4 |
| ΔZГ оп ср, M | 0,343 | 0,322 | 0,4 |
Результаты исследования точности построения блочной сети фототриангуляции в зависимости от числа точек в стереопарах приведены в таблице 4.2 Как видно максимальный остаточный поперечный параллакс и СКО остаточного поперечного параллакса наблюдается при наличии 3 точек в каждой стандартной зоне и при уменьшении их до 2 результаты улучшаются, при последующем сокращении до1 эти показатели несколько увеличиваются но всё равно они меньше чем в первом варианте. Объясняется это тем, что мы убирали самые «плохие» точки, но на самом деле при наличии большего числа точек результат должен улучшится.
Таблица 4.2- Оценка точности построения блочной ПФТ при разном количестве точек в шести стандартных зонах.
| Этап ПФТ | Апостериорная оценка точности | Допуски по инструкции | ||
| Количество точек в стандартной зоне | ||||
| 3 | 2 | 1 | ||
| Взаимное ориентирование снимков | ||||
| δqmax , MM | 0,0036 | 0,0035 | 0,0036 | - |
| mδq , MM | 0,0018 | 0,0019 | 0,0019 | 0,01 |
| Подсоединение моделей | ||||
| Δxсв max , MM | 0,00069 | 0,00075 | 0,00076 | - |
| Δyсв max , MM | 0,00279 | 0,00287 | 0,00310 | - |
| Δzсв max , MM | 0,00991 | 0,01015 | 0,01036 | - |
| mΔxсв, MM | 0,00025 | 0,00029 | 0,0003 | 0,015 |
| mΔyсв, MM | 0,00141 | 0,00145 | 0,00152 | 0,015 |
| mΔzсв, MM | 0,00512 | 0,00518 | 0,00557 | 0,046 |
| Уравнивание сети ПФТ | ||||
| ΔXоп max , M |
0,328 ,, |
0,354 | 0,375 | 0,8 |
| ΔYоп max , M | 0,407 | 0,332 | 0,327 | 0,8 |
| ΔZоп max , M | 0,585 | 0,585 | 0,598 | 0,8 |
| mΔX оп, M | 0,183 | 0,181 | 0,195 | 0,5 |
| mΔYоп, M | 0,218 | 0,199 | 0,180 | 0,5 |
| mΔZоп, M | 0,372 | 0,370 | 0,357 | 0,5 |
| ΔLГ max , M | 0,257 | 0,256 | 0,254 | 0,4 |
| mΔLГ, M | 0,283 | 0,279 | 0,265 | 0,5 |
| ΔXГ оп ср , M | 0,155 | 0,161 | 0,163 | 0,4 |
| ΔYГ оп ср , M | 0,161 | 0,158 | 0,140 | 0,4 |
| ΔZГ оп ср , M | 0,343 | 0,332 | 0,322 | 0,4 |
Результаты исследования точности построения блочной сети фототриангуляции в зависимости от числа и расположения опорных точек в сети приведены в таблице 4.3. Как видно из схемы 1 в первом варианте расположения опорных точек, они расположены по всему блоку почти равномерно, все контрольные величины удовлетворяют допуску. Расположение опорных точек по схеме 2 дало наихудший результат, причиной такого результата является то, что блок по краям не обеспечен опорными точками и тем, что опорных точек было меньше чем в схеме 1 и схеме2. Лучший результат получился при расположении опорных точек по схеме 3 это можно объяснить тем, что грубо измеренные точки были исключены из уравнивания.
Таблица 4.3- Оценка точности построения блочной ПФТ при различном количестве и расположении опорных точек.
| Этап ПФТ | Апостериорная оценка точности | Допуски по инструкции | ||
| Схема 1 | Схема 2 | Схема 3 | ||
| ΔXоп max, M |
0,328 0,206 |
0,315 | 0,357 | 0,8 |
| ΔYоп max , M | 0,407 | 0,185 | 0,250 | 0,8 |
| ΔZоп max , M | 0,585 | 0,119 | 0,646 | 0,8 |
| mΔX оп max , M | 0,183 | 0,174 | 0,206 | 0,5 |
| mΔYоп max , M | 0,216 | 0,119 | 0,137 | 0,5 |
| mΔZоп max , M | 0,372 | 0,075 | 0,359 | 0,5 |
| ΔLГ max , M | 0,257 | 0,196 | 0,222 | 0,4 |
| mΔLГ max , M | 0,283 | 0,211 | 0,247 | 0,5 |
| ΔXГ оп ср , M | 0,155 | 0,145 | 0,177 | 0,4 |
| ΔYГ оп ср , M | 0,161 | 0,110 | 0,111 | 0,4 |
| ΔZГ оп ср , M | 0,343 | 0,066 | 0,278 | 0,4 |
Схема 1
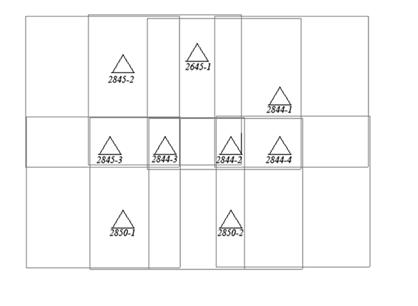
Схема 2
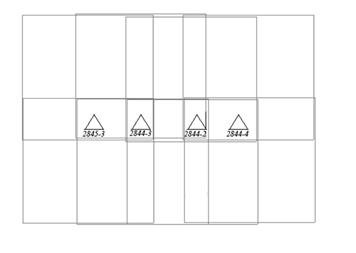
Схема 3
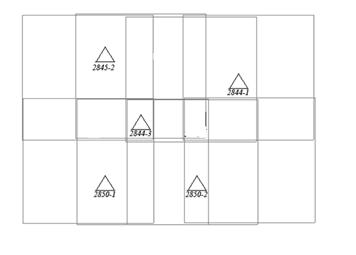
В результате проделанной исследовательской работы мною было установлено, что манипуляции со связующими точками(избыток или недостаток) существенно не влияет на результат. Опорные точки наихудшие результаты показывают при уравнивании когда опорные точки оставлены по прямой, что и следовало ожидать так как по краям в этом случае идет искажение. При изменении способа уравнивания также не было особых изменений, хотя метод независимых моделей имеет немного лучший результат. Результаты данного исследования не являются надёжными так-так из-за малого размера обрабатываемого блока в обработке участвовало небольшое количество точек и поэтому не факт, что полученный результат является закономерностью.
Заключение
В результате выполнения курсовой работы:
- рассмотрено понятие пространственной цифровой фототриангуляции, назначение, достоинства, основные методы, а также её особенности;
- рассмотрена краткая характеристика ЦФС «Фотомод» и технология построения блочной сети фототриангуляции на ЦФС «Фотомод»;
- подробно рассмотрено построение блочной сети фототриангуляции на ЦФС «Фотомод», включающее оценку фотографического и фотограмметрического качества исходных материалов, составление рабочего проекта, подготовку исходных данных для построения сети, внутреннее ориентирование снимков, измерение плоских координат опорных, межмаршруных и связующих точек снимков, построение и уравнивание блочной сети фототриангуляции, оценку точности, контроль качества и анализ результатов цифровой фототриангуляции;
- проведены исследования точности построения блочной сети фототриангуляции, которые показали, что точность её построения зависит от числа точек в стереопарах, от числа и расположения опорных точек в сети и от используемого метода уравнивания сети.
Таким образом были изучены теоретические основы и получены практические навыки построения сетей пространственной фототриангуляции по результатам аэрофотосъемки с использование ЦФС «Фотомод».
Список использованных источников
1. Антипов, И.Т. Математические основы пространственной аналитической фототриангуляции [Текст] / И.Т. Антипов. – М.:Картгеоцентр-Геодезиздат, 2003. – 296 с.
2. Гук, А.П. Аналитическая фототриангуляция с применением микро-ЭВМ и ЭВМ “ЕС-1022” [Текст]: Учебное пособие / А.П. Гук, Т.А. Широкова. – Новосибирск, 1987. – 82 с.
3. Инструкция по фотограмметрическим работам при создании цифровых топографических карт и планов [Текст] – М., 2002. – 100с.
4. Основные положения по аэрофотосъемке, выполненной для создания и обновления топографических карт и планов ГКИНП-09-32-80 [Текст] – М.: Недра, 1982. – 16 с.
5. Пособие по ЦФС “Фотомод” в электронном виде.
6. Лобанов, А.Н. Фотограмметрия [Текст]: Учебник для вузов / А.Н. Лобанов. – М.:Недра, 1984. – 552 с.
Перепечатка материалов без ссылки на наш сайт запрещена