Курсовая работа: Критерій відношення правдоподібності для великих вибірок

Курсовая работа: Критерій відношення правдоподібності для великих вибірок

Міністерство освіти і науки України

Національний Університет "Львівська Політехніка"

Інститут прикладної математики та фундаментальних наук

Кафедра прикладної математики

Курсова робота

з курсу математичної статистики

на тему:

"Критерій відношення правдоподібності для великих вибірок"

Керівник роботи

доц. каф. ПМ Ружевич Н. А.

Виконав студент гр. ПМ-41

Новосад Н.

Львів – 2009

Розглянуто один із методів перевірки параметричних статистичних гіпотез – метод відношення правдоподібності для великих вибірок. Наведено теоретичне обґрунтування даного методу, проілюстровано його застосування до розв’язку практичних задач. Виконано програмну реалізацію методу.

Зміст

Вступ

1.  Основні поняття

2.  Критерій відношення правдоподібності для великих вибірок

3.  Приклади застосування критерію відношення правдоподібності для великих вибірок

4.  Опис програми

Висновки

Список використаної літератури

Додаток А. Використані статистичні таблиці

Додаток B. Текст програми, що реалізує застосування критерію відношення правдоподібності для великих вибірок

Додаток C. Результати виконання програми

Вступ

Математична статистика – це один з розділів математики, що має широке прикладне значення в науці і техніці. Зокрема, методи математичної статистики широко використовуються в теорії масового обслуговування, теорії надійності, теорії інформації, стохастичній апроксимації та інших дисциплінах.

Одним із основних інструментів математичної статистики є теорія перевірки статистичних гіпотез. Причиною виникнення цієї теорії стала проблема визначення закономірностей розподілу випадкових величин( їхніх функцій та щільностей розподілу), основних характеристик( математичного сподівання, дисперсії та ін.), залежностей між випадковими величинами.

Як зрозуміло із самої назви, теорія перевірки статистичних гіпотез займається розробкою та обґрунтуванням методів перевірки статистичних гіпотез. Під статистичною гіпотезою розуміють припущення щодо виду розподілу випадкової величини, незалежності випадкових величин, значень невідомих параметрів розподілу та ін. на основі експериментальних статистичних даних.

На сьогоднішній день розроблено багато методів перевірки гіпотез( критеріїв згоди), що застосовуються на практиці. Одним із таких критеріїв є критерій відношення правдоподібності для великих вибірок. Саме цей метод розглянуто у даній курсовій роботі.

Структуру курсової роботи складають п’ять розділів і чотири додатки. У розділі "Основні поняття" введено необхідні поняття та позначення, які будуть використовуватись у подальшому. У розділі "Критерій відношення правдоподібності для великих вибірок" описано суть критерію. У розділі "Приклади застосування критерію відношення правдоподібності для великих вибірок" на декількох прикладах проілюстровано застосування цього критерію до практичних задач. У пункті "Висновки" обговорюється практична цінність критерію, а також його недоліки. Далі наводиться список використаної літератури і статистичних таблиць, дані з яких використовувались. У додатках В , С та D наводиться опис, код та результати роботи програми, яка реалізує перевірку гіпотези на основі розглянутого критерію.

1. Основні поняття

Введемо ряд понять та означень, які будемо використовувати в подальшому.

Через  будемо позначати функцію, що визначена на деякому ймовірнісному просторі  і називається випадковою величиною, де це непорожня множина, що називається простором елементарних подій, а елементи  називаються елементарними подіями(вважається, що  складається з усіх можливих результатів експерименту і результатом будь-якого експерименту може бути лише один елемент ); це деяка система підмножин , яка утворює  алгебру, тобто для неї виконується така система умов:

1) 

2) 

3) 

4) 

5)  Тоді множини  називаються подіями. це відображення подій  на інтервал , яке задовольняє наступним аксіомам:

1)   поставлено у відповідність число  і називається ймовірністю події

2) 

3) 

Відображення  називається ймовірністю простору .

Нехай в результаті проведення експерименту спостерігаються значення  випадкових величин  Тоді вектор, компонентами якого є ці випадкові величини , називається вибіркою, а об’ємом вибірки. Вектор  де це значення, яке набула випадкова величина  внаслідок проведення експерименту, називається реалізацією вибірки. Множина всіх можливих реалізацій вибірки  називається вибірковим простором.

Нехай випадкова величина і деяке дійсне значення. Тоді ймовірність того, що випадкова величина  приймає значення менше за називається функцією розподілу ймовірностей випадкової величини  і позначається  Якщо функція розподілу залежить від деякого параметра , то писатимемо  Клас функцій розподілу  називатимемо класом допустимих розподілів спостережуваної випадкової величини  і позначатимемо . Множина  така, що  і називається параметричною множиною. Той факт, що випадкова величина  має функцію розподілу з класу  будемо позначати  і називати розподілом випадкової величини. Статистичною моделлю експерименту називається впорядкована пара  де вибірковий простір випадкової величини клас розподілів цієї випадкової величини. Статистикою називають будь-яку випадкову величину, що залежить лише від вибірки . Статистика  називається оцінкою невідомого параметра  розподілу  , якщо для кожної реалізації вибірки значення  приймається за наближене значення параметра . Статистика  називається незміщеною оцінкою параметра , якщо (тут  - це математичне сподівання, тобто , якщо випадкова величина  має неперервну функцію розподілу( у цьому випадку  у точках існування похідної, і називається функцією щільності ), і  у дискретному випадку( тобто  набуває не більш, ніж зліченної кількості значень  відповідно з ймовірностями , не більш, ніж зліченна множина і  )). Позначимо через клас незміщених оцінок для параметра . Тоді, оптимальною оцінкою параметра  називається така статистика , що

де  і називається дисперсією випадкової величини .

Нехай щільність розподілу випадкової величини ( або ймовірність – у дискретному випадку), вибірка з розподілу ( тобто всі  мають розподіл  і є незалежними випадковими величинами), реалізація вибірки. Функція  є щільністю розподілу випадкового вектора . Якщо розглядається при фіксованому значенні , то така функція параметра  називається функцією правдоподібності. Оцінкою максимальної правдоподібності невідомого параметра  називається таке значення , при якому  для заданого .

Статистичною гіпотезою( або просто гіпотезою) називають будь-яке твердження щодо виду чи властивостей розподілу спостережуваної випадкової величини. Статистичні гіпотези надалі позначатимемо так: . Статистичною параметричною гіпотезою називається припущення про значення невідомого параметра  розподілу  Наведемо приклади параметричних гіпотез:

1) 

2) 

3)   де взагалі кажучи, деяка векторна функція , стала.

В загальному випадку параметрична гіпотеза задається деякою підмножиною , до якої, за припущенням, належить невідомий параметр . Тоді параметрична гіпотеза записується так: . Альтернативна гіпотеза має вигляд: ; точки називаються альтернативами. Якщо множина  містить лише одну точку, то гіпотезу( альтернативу ) називають простою; у протилежному випадку гіпотезу( альтернативу) називають складною.

Правило, згідно якого висунута гіпотеза  приймається або відкидається, називається статистичним критерієм( або просто критерієм) перевірки гіпотези .

Нехай вибірка з розподілу  і висунута параметрична гіпотеза ( може бути як скаляром, так і вектором і надалі будемо вважати його вектором, якщо не обумовлено протилежне). Потрібно визначити чи узгоджується запропонована гіпотеза із результатами проведеного експерименту. У такому випадку поступають наступним чином: будують таке правило( критерій), яке дозволяє на основі отриманих реалізацій вибірки  зробити висновок: прийняти гіпотезу  чи відхилити її( прийняти альтернативу ). Отже, критерій розбиває вибірковий простір  на дві множини  такі, що , де  складається із тих точок, для яких гіпотеза  приймається, а множина із точок, для яких  відхиляється. Множина  називається областю прийняття гіпотези, а множина  називається областю відхилення гіпотези, або критичною областю.

У процесі перевірки гіпотези  можна прийти до правильного висновку або допустити помилку першого роду – відхилити , коли гіпотеза вірна, чи помилку другого роду – прийняти , коли вона хибна.

Ймовірності цих двох помилок можна виразити через функцію потужності  критерію : . А саме: ймовірність похибки першого роду рівна , а ймовірність похибки другого роду рівна .

Число  називають рівнем значущості критерію, якщо .

Нехай , тоді квантилем  розподілу  називається корінь рівняння . Якщо функція  строго монотонна, то це рівняння має єдиний корінь; у протилежному випадку це рівняння має декілька коренів, і тоді квантилем називають мінімальний серед коренів рівняння.

2. Критерій відношення правдоподібності для великих вибірок

Одним із найбільш універсальних методів побудови критеріїв перевірки складних гіпотез є метод відношення правдоподібності, суть якого полягає у наступному. Для перевірки гіпотези  проти альтернативи  вводиться статистика відношення правдоподібності

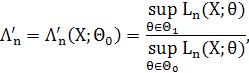
де , функція правдоподібності. Разом із статистикою  вводиться статистика

Будемо вважати, що виконуються умови регулярності, що забезпечують існування, єдність і асимптотичну нормальність оцінки максимальної правдоподібності  параметра . Розглянемо випадок простої гіпотези.

Теорема. Нехай потрібно перевірити просту гіпотезу фіксована внутрішня точка множини . Тоді для великих вибірок( ) при виконанні вказаних умов регулярності критерію відношення правдоподібності задається асимптотично критичною множиною

(1)

тобто при

де рівень значущості критерію.

Доведення. Покажемо, що з умов теореми слідує:

(2)

звідки випливає рівність (1). Якщо справедлива гіпотеза , то в силу спроможності оцінки максимальної правдоподібності при великих  точка близька до , тому для  можна записати розклад Тейлора відносно точки :

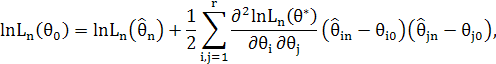
де Звідси випливає, що

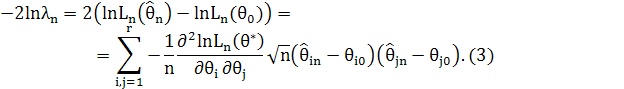
Оскільки слушна оцінка для , а другі похідні функції правдоподібності, за припущенням, неперервні по , то справедливо:

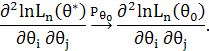
На основі закону великих чисел при  величина

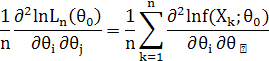
збігається за ймовірністю( за розподілом ) до середнього значення

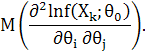
Таким чином, матриця граничних значень коефіцієнтів квадратичної форми у (3) співпадає з інформаційною матрицею . Звідси слідує, що випадковий вектор  має в границі такий же розподіл, як і нормальний  випадковий вектор  Таким чином, права частина (3) має в границі такий розподіл, як і квадратична форма . Тоді . Звідки і випливає співвідношення (2). Теорему доведено.

Розглянемо важливий приклад застосування викладених результатів до поліноміального розподілу

Приклад( метод відношення правдоподібності для поліноміального розподілу). Нехай проводяться незалежні випробування, в кожному з яких реалізується один із  можливих наслідків , тобто спостерігається випадкова величина , що приймає значення (, якщо наступила подія ). Позначимо через вектор ймовірностей цих подій( ) і через  вектор частот реалізацій відповідних наслідків в  випробуваннях( ). Як відомо, розподіл вектора  має поліноміальний розподіл . Припустимо тепер, що ймовірності подій  невідомі і потрібно перевірити гіпотезу  де заданий вектор, що задовольняє умовам: . Альтернативна гіпотеза має вигляд .

Тут роль параметра  відіграє вектор , але оскільки на значення параметрів накладена вимога , то бажано позбутись цього обмеження, виключивши, наприклад,. Таким чином, надалі покладаємо  і .

Оцінками максимальної правдоподібності для параметрів  є відносні частоти реалізацій відповідних подій, тобто , тому в даному випадку статистика відношення правдоподібності має вигляд:

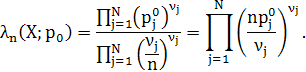
Звідси

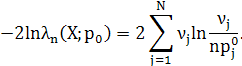
Якщо справедлива гіпотеза , то в границі при  ця статистика має розподіл , тому при заданому рівні значущості  критичну границю вибирають рівною . Тоді критична множина матиме вигляд: , причому критична точка  визначається із співвідношення:

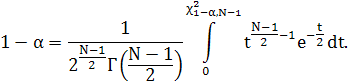
Тому, якщо

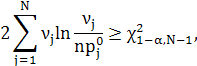
то гіпотеза  відхиляється( тобто вона не узгоджується із статистичними даними проведеного експерименту, і ймовірність того, що ми відхиляємо правильну гіпотезу не перевищує значення ), у протилежному випадку – приймається.

Приклад 2(метод відношення правдоподібності для перевірки значень параметрів нормального розподілу)

Розглядається вибірка з нормального розподілу. Потрібно перевірити гіпотезу про значення параметрів нормального розподілу за двосторонньої альтернативи. А саме, , альтернативна гіпотеза. Обчислимо статистику критерію. Для цього знайдемо функцію правдоподібності для нормального розподілу  . Тоді

.

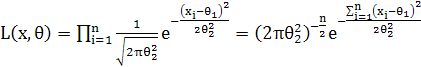Звідси,

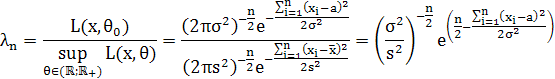
Тут,. Тому статистика критерію матиме вигляд:

.

У наступному розділі ми більш детально розглянемо застосування критерію відношення правдоподібності для великих вибірок до перевірки статистичних гіпотез.

3. Приклади застосування критерію відношення правдоподібності для великих вибірок

Розглянемо декілька прикладів на застосування розглянутого критерію.

Приклад 1. Кількість бракованих деталей у партії не повинна перевищувати . У результаті контролю 100 деталей із цієї партії виявлено 6 бракованих. Чи можна вважати, що відсоток браку рівний  при ?

Розв’язання. Для розв’язку задачі застосуємо критерій відношення правдоподібності для великих вибірок. Нехай ймовірність браку деталі, ймовірність того, що деталь справна,.  - припущення про параметр розподілу. Отже, перевіримо просту гіпотезу , тоді альтернативна гіпотеза  тут У нашому випадку , тоді статистика критерію

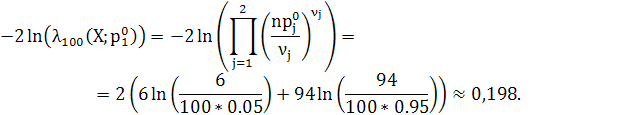
Для заданого рівня значущості  знаходимо критичну точку ( див. Додаток А). Отже, отримали, що при даній реалізації вибірки статистика критерію отримала значення , яке менше критичного значення , тобто гіпотеза  приймається, а тому відсоток браку можна вважати таким, що рівний .

Приклад 2. Гральний кубик підкинули 600 разів, при цьому шестірка випала 75 разів, п’ятірка – 118, четвірка – 124, трійка – 108, двійка – 92 і одиничка - 83. Чи можна вважати, що кубик симетричний і однорідний? Прийняти

Розв’язання. У цій задачі невідомий параметр, причому ,  Тоді . Гіпотеза , альтернатива . Знайдемо значення статистики критерію

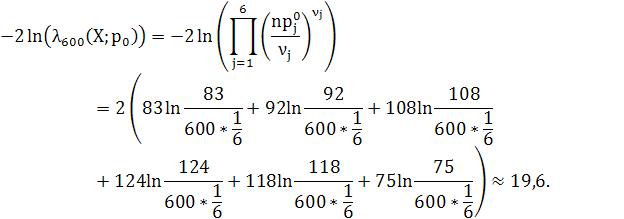
Критична точка . Оскільки, то гіпотеза  відхиляється, тому не можна вважати, що кубик симетричний і однорідний.

Приклад 3. Метод одержання випадкових чисел був застосований 250 разів, при цьому отримали наступні результати:

Цифра	0	1	2	3	4	5	6	7	8	9
Частота появи	27	18	23	31	21	23	28	25	22	32

Чи можна вважати, що застосований метод дійсно генерує випадкові числа? Покласти  Розв’язання. Згідно умови задачі,  невідомий параметр, ,  Тоді . Гіпотеза , альтернатива . Знайдемо значення статистики критерію:

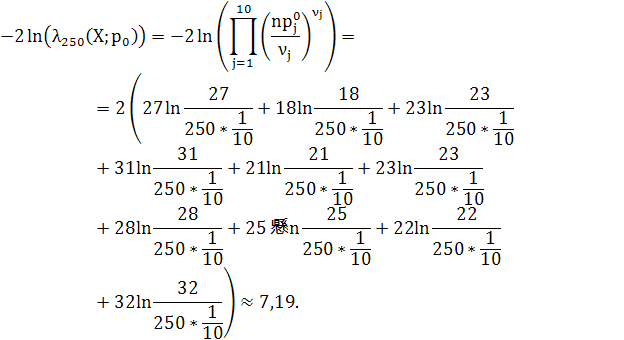
Критична точка множини . Отже, , тому гіпотеза  приймається. Тому можна вважати, що застосований метод справді генерує випадкові числа.

4. Опис програми

Призначення програми. Використовуючи програму, код модуля якої наведений у додатку B, можна розв’язувати задачі на узгодженість простої параметричної гіпотези із реалізаціями великих вибірок. Перевірка узгодженості проводиться на основі критерію відношення правдоподібності для великих вибірок. Умови застосування. Програма коректно працює на IBM – сумісних комп’ютерах з такими характеристиками: Celeron 2.26/MB ASUS P4VM-800 /DDR 1.5Gb PC3200/ HDD 330 Gb 7200 rpm/ Radeon 9250 128/128, під операційною системою – Windows XP Professional SP3 із встановленим програмним забезпеченням – середовищем розробки - Delphi 7.

Опис задачі та вихідні дані. У додатку C наводяться три результати виконання програми. У першому випадку при вводі даних вручну потрібно вказати у відповідні поля кількість різних значень випадкової величини та рівень значущості. У таблицю вводяться частоти і ймовірності, з якими випадкова величина набуває відповідні значення. У другому випадку розглядається подібна задача, тільки тут дані зчитуються з файлу. У третьому випадку програма сама генерує вибірку з нормального розподілу і перевіряється гіпотеза про значення математичного сподівання і дисперсії цього розподілу, причому на формі вказується значення математичного сподівання, дисперсії і рівня значущості. Текст програми. У додатку B наведений код модуля програми, оскільки при написанні програми використано візуальне середовище Delphi 7. Результати. У додатку C наведені результати виконання програми на різних контрольних прикладах.

Висновки

У курсовій роботі було розглянуто один із критеріїв відношення правдоподібності, а саме: критерій відношення правдоподібності для великих вибірок, його теоретичне обґрунтування, застосування до розв’язування практичних задач. Проте, як і будь-який інший статистичний критерій, він має свої переваги і недоліки, які визначають його практичну цінність. Тому розглянемо їх.

Критерії відношення правдоподібності мають широке практичне застосування з огляду на такі їхні властивості( які мають місце у широкому класі задач), як:

1.  Критерії відношення правдоподібності є найбільш потужними серед усіх інших можливих критеріїв( лема Неймана - Пірсона).

2.  Щільність розподілу критичної статистики можна легко отримати із функції правдоподібності спостережуваної випадкової величини( у випадку застосування цих критеріїв до перевірки гіпотез для великих вибірок, користуються асимптотичною щільністю хі -квадрат розподілу).

Однак, варто відзначити, що ці критерії мають ряд недоліків, які дещо звужують коло застосувань цих методів. Одним із головних недоліків є вимога регулярності функцій правдоподібності, що не завжди має місце на практиці. Інші два недоліки мають місце при застосуванні будь-яких статистичних критеріїв. Це так звані ефекти "надто малого об’єму вибірки" та ефекти "надто великого об’єму вибірки".

Ефект " надто малого об’єму вибірки" полягає у тому, що при заданому рівні значущості критерію  і малій кількості спостережень( ), на основі яких отримують потужність критерію, тобто ймовірність відхилити нульову гіпотезу  у випадку, коли вона насправді хибна, є дуже малою. У такому випадку застосовують два підходи: або дещо збільшують значення рівня значущості критерію ( що, у свою чергу, призводить до зменшення похибки другого роду, але одночасного збільшення похибки першого роду), або збільшують об’єм вибірки .

Ефект "надто великого об’єму вибірки" полягає у тому, що при великих значеннях  надзвичайно сильно зростає чутливість критерію до емпіричних результатів, і в таких випадках висунута гіпотеза практично завжди відхиляється критерієм. Для того, щоб уникнути ефекту великої вибірки, апріорне визначення характеристик критерію( рівня значущості  і похибки другого роду ) потрібно пов’язувати з об’ємом вхідних даних . Виграш у чутливості критерію, який отримується при зростанні , доцільно використати для зменшення як , так і . Зокрема, якщо при збільшенні  зменшувати , то дуже малі відхилення від  вже не приведуть до обов’язкової неузгодженості  з емпіричними даними: ймовірність цього факту буде залежати від того, з якою швидкістю зменшується  при зростанні .

Список використаної літератури

1.  Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. Справочное пособие. – М.: Финансы и статистика, 1983. – 471 с.

2.  Ефимов А.В. Сборник задач по математике для втузов. Специальные курсы. Т.3. – М.: Наука, 1984. – 608 с.

3.  Ивченко Г.И., Медведев Ю.И. Математическая статистика. – М.: Высш. шк., 1984. – 248 с.

4.  Ружевич Н.А. Математична статистика. – Львів: Львівська політехніка, 2001. – 168 с.

Додаток А. Використані статистичні таблиці

Таблиця значень  квантилей для хі – квадрат розподілу з  ступенями вільності

0,1	0,3	0,5	0,7	0,9	0,95	0,999	0,9999
0,016	0,148	0,455	1,07	2,71	3,84	6,63	10,8
0,211	0,713	1,39	2,41	4,61	5,99	9,21	13,8
0,584	1,42	2,37	3,67	6,25	7,82	11,3	16,3
1,06	2,20	3,36	4,88	7,78	9,49	13,3	18,5
1,61	3,00	4,35	6,06	9,24	11,1	15,1	20,5
2,20	3,83	5,35	7,23	10,6	12,6	16,8	22,5
2,83	4,67	6,35	8,38	12,0	14,1	18,5	24,3
3,49	5,53	7,34	9,52	13,4	15,5	20,1	26,1
4,17	6,39	8,34	10,7	14,7	16,9	21,7	27,9
4,87	7,27	9,34	11,8	16,0	18,3	23,2	29,6
5,58	8,15	10,3	12,9	17,3	19,7	24,7	31,3
6,30	9,03	11,3	14,0	18,5	21,0	26,2	32,9
7,04	9,93	12,3	15,1	19,8	22,4	27,7	34,5
7,79	10,08	13,3	16,2	21,1	23,7	29,1	36,1
8,55	11,7	14,3	17,3	22,3	25,0	30,6	37,7
9,31	12,6	15,3	18,4	23,5	26,3	32,0	39,3
10,09	13,5	16,3	19,5	24,8	27,6	33,4	40,8
10,9	14,4	17,3	20,6	26,0	28,9	34,8	42,3
11,7	15,4	18,3	21,7	27,2	30,1	36,2	43,8
12,4	16,3	19,3	22,8	28,4	31,4	37,6	45,3
13,2	17,2	20,3	23,9	29,6	32,7	38,9	46,8
14,0	18,1	21,3	24,9	30,8	33,9	40,3	48,3
14,8	19,0	22,3	26,0	32,0	35,2	41,6	49,7
15,7	19,9	23,3	27,1	33,2	36,4	43,0	51,2
16,5	20,9	24,3	28,2	34,3	37,7	44,3	52,6
17,3	21,8	25,3	29,2	35,6	38,9	45,6	54,1
18,1	22,7	26,3	30,3	36,7	40,1	47,0	55,5
18,9	23,6	27,3	31,4	37,9	41,3	48,3	56,9
19,8	24,6	28,3	32,5	39,1	42,6	49,6	58,3
20,6	25,5	29,3	33,5	40,3	43,8	50,9	59,7

Додаток B. Текст програми, що реалізує застосування критерію відношення правдоподібності для великих вибірок

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Grids, ExtCtrls, Math;

type

TFrm = class(TForm)

GrpBox_HandEnter: TGroupBox;

RdoGrp_CaseEnter: TRadioGroup;

RdBtn_FileRead: TRadioButton;

RdBtn_HandEnter: TRadioButton;

StrGrd: TStringGrid;

Lbl_LevelMean: TLabel;

Cmb_LevelMean: TComboBox;

Lbl_CountValue: TLabel;

Cmb_CountValue: TComboBox;

GrpB_Result: TGroupBox;

Memo_WriteResult: TMemo;

Button1: TButton;

OpnDg: TOpenDialog;

RdB_CompGenerate: TRadioButton;

Edt_Average: TEdit;

Edt_Dispersion: TEdit;

Lbl_Average: TLabel;

Lbl_Dispersion: TLabel;

procedure Button1Click(Sender: TObject);

procedure RdBtn_HandEnterClick(Sender: TObject);

procedure Cmb_CountValueChange(Sender: TObject);

procedure RdBtn_FileReadClick(Sender: TObject);

procedure RdB_CompGenerateClick(Sender: TObject);

procedure Edt_AverageChange(Sender: TObject);

procedure Edt_DispersionChange(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Frm: TFrm;

List:TStringList;

implementation

{$R *.dfm}

Function Factorial(N:Integer):Integer;

var s:Integer;

begin

s:=1;

if(N>0) then

while (N>0) do

begin

s:=N*s;

N:=N-1;

end;

Result:=s;

end;

function FactorialHalf(N:Integer):Double;

var s:Double;

begin

s:=1;

if(N>=0) then

begin

while (N>=0) do

begin

s:=(1./2+N)*s;

N:=N-1;

end;

end;

Result:=s;

end;

Function Abs(s:Double):Double;

begin

if(s>0) then

Abs:=s

else

Abs:=-s;

end;

function FindCriticalPoint(N: Integer): Double;

var Gamma,Integral,c, h,level_mean: Double;

i: Integer; NumPointsIntegrate:LongInt;

begin

c:=0.1; i:=0; Integral:=0;h:=c/2;

level_mean:= StrToFloat(Frm.Cmb_LevelMean.Text);

NumPointsIntegrate:=1000;

if(((N-1) mod 2)=1) then

Gamma:=Power(ArcCos(-1),1./2)*FactorialHalf(((N-1)div 2)-1)

else

Gamma:=Factorial(((N-1) div 2)-1);

while(Abs(((1-level_mean) -Integral/(Gamma*Power(2,0.5*(N-1)))))>0.00001) do

begin

Integral:=0;

for i:=1 to NumPointsIntegrate do

Integral:=Integral+ (c/(NumPointsIntegrate))*Power(i*c/(NumPointsIntegrate),(0.5*N-1.5))*exp(-i*c/(2*NumPointsIntegrate));

if ((((1-level_mean) )-Integral/(Gamma*Power(2,0.5*(N-1)))))>0 then

begin

c:=c+h ;

NumPointsIntegrate:=NumPointsIntegrate+100;

end

else

begin

c:=c-h;

h:=h/10;

c:=c+h;

end;

end;

FindCriticalPoint:=c;

end;

function EvaluteStatistic(aOfValues:Array of Double; aOfProbabil:Array of Double; CountVal:Integer; f:Boolean):Double;

var i,n:Integer;

s,sum,s_2,disp,aver:Double;

begin

s:=0; n:=0;

sum:=0;

if(not f) then

begin

for i:=0 to CountVal-1 do

sum:=sum+aOfValues[i];

for i:=0 to CountVal-1 do

s:=s+2*aOfValues[i]*LnXP1(aOfValues[i]/(sum*aOfProbabil[i])-1);

Result:=s;

end

else

begin

for i:=1 to Frm.StrGrd.ColCount-1 do

if(Frm.StrGrd.Cells[i,2]<>'') then

begin

s:=s+Power(StrToFloat(Frm.StrGrd.Cells[i,1]),2);

sum:=sum+StrToFloat(Frm.StrGrd.Cells[i,1]);

n:=n+StrToInt(Frm.StrGrd.Cells[i,2]);

end;

s_2:=(s/n)-Power(sum/n,2);

disp:= StrToFloat(Frm.Edt_Dispersion.Text);

aver:= StrToFloat(Frm.Edt_Average.Text);

Result:=n*LnXP1((disp/s_2)-1)-n+s/disp-2*sum*aver/disp+n*Power(aver,2)/disp;//n*LnXP1((disp/s_2)-1);

end;

end;

procedure TFrm.Button1Click(Sender: TObject);

var ValArr:array of Double; ProbArray:array of Double;

i:Integer; s:TStringList; st,critical_point:Double;

begin

if(RdBtn_HandEnter.Checked ) then

begin

SetLength(ValArr,StrGrd.ColCount-1);

SetLength(ProbArray,StrGrd.ColCount-1);

For i:=0 to StrGrd.ColCount-2 do

begin

try

ValArr[i]:=StrToFloat(StrGrd.Cells[i+1,1]);

ProbArray[i]:= StrToFloat(StrGrd.Cells[i+1,2]);

finally end;

end;

end

else

if (RdBtn_FileRead.Checked ) then

begin

s:= TStringList.Create;

s.Text:=StringReplace(List[0],' ',#13#10,[rfReplaceAll]);

SetLength(ValArr,s.Count);

Cmb_CountValue.Text := IntToStr(s.Count );

RdBtn_HandEnter.Checked :=false;

for i:=0 to s.Count-1 do

ValArr[i]:=StrToFloat(s[i]);

s.Text:=StringReplace(List[1],' ',#13#10,[rfReplaceAll]);

SetLength(ProbArray,s.Count);

for i:=0 to s.Count -1 do

ProbArray[i]:=StrToFloat(s[i]);

end;

Memo_WriteResult.Lines.Clear();

Memo_WriteResult.Lines.Add('Значення статистики критерію:');

if(RdBtn_HandEnter.Checked ) then

begin

st:=EvaluteStatistic(ValArr, ProbArray, StrGrd.ColCount-1,false);

Memo_WriteResult.Lines.Add(FloatToStr(st));

end

else

if (RdBtn_FileRead.Checked ) then

begin

st:=EvaluteStatistic(ValArr, ProbArray,s.Count,false );

Memo_WriteResult.Lines.Add(FloatToStr(st));

end

else

begin

st:=EvaluteStatistic(ValArr, ProbArray,0,true);

Memo_WriteResult.Lines.Add(FloatToStr(st));

end;

Memo_WriteResult.Lines.Add('Значення критичної точки:');

if(RdB_CompGenerate.Checked )then

critical_point:=FindCriticalPoint(3)

else

critical_point:=FindCriticalPoint(StrToInt(Frm.Cmb_CountValue.Text));

Memo_WriteResult.Lines.Add(FloatToStr(critical_point));

if(st<critical_point) then

Memo_WriteResult.Lines.Add('Висновок: гіпотеза не суперечить реалізації вибірки.')

else

Memo_WriteResult.Lines.Add('Висновок: гіпотеза суперечить реалізації вибірки.');

end;

procedure TFrm.RdBtn_HandEnterClick(Sender: TObject);

var i:Integer;

begin

Memo_WriteResult.Lines.Clear();

Edt_Average.Visible:=false; Lbl_Average.Visible:=false;Cmb_CountValue.Visible:=true;

Edt_Dispersion.Visible: = false; Lbl_Dispersion. Visible: = false;Lbl_CountValue.Visible :=true;

StrGrd.ColCount:=StrToInt(Cmb_CountValue.Text )+1;

for i:=1 to StrGrd.ColCount do

StrGrd.Cols[i].Text:='x'+IntToStr(i);

StrGrd.RowCount:=3;

StrGrd.Rows[1].Text:='Частоти';

StrGrd.Rows[2].Text:='Ймовірності';

end;

procedure TFrm.Cmb_CountValueChange(Sender: TObject);

begin

RdBtn_HandEnterClick( Sender);

RdBtn_HandEnter.Checked:=true;

end;

procedure TFrm.RdBtn_FileReadClick(Sender: TObject);

begin

Memo_WriteResult.Lines.Clear();

Edt_Average.Visible:=false; Lbl_Average.Visible:=false;Cmb_CountValue.Visible:=false;

Edt_Dispersion.Visible:= false; Lbl_Dispersion.Visible:=false;Lbl_CountValue.Visible :=false;

List:= TStringList.Create;

if OpnDg.Execute then

List.LoadFromFile(OpnDg.FileName );

end;

function SetGaussNumber(a:String):Boolean;

var i:Integer;

begin

SetGaussNumber:=false;

for i:=1 to Frm.StrGrd.ColCount-1 do

begin

if( Frm.StrGrd.Cells[i,0]<>'') then

begin

if(Frm.StrGrd.Cells[i,2]='') then

Frm.StrGrd.cells[i,2]:='1';

if(Frm.StrGrd.Cells[i,1]=a) then

begin

Frm.StrGrd.cells[i,2]:=IntToStr(StrToInt(Frm.StrGrd.cells[i,2])+1);

SetGaussNumber:=true;

end

end;

end;

end;

procedure TFrm.RdB_CompGenerateClick(Sender: TObject);

var i:Integer;

begin

Memo_WriteResult.Lines.Clear();

Randomize;

StrGrd.Rows[1].Text:='Значення';

StrGrd.Rows[2].Text:='Частоти';

Edt_Average.Visible:=true; Lbl_Average.Visible:=true;Cmb_CountValue.Visible:=false;

Edt_Dispersion.Visible:= true; Lbl_Dispersion.Visible:=true;Lbl_CountValue.Visible :=false;

for i:=0 to 50 do

begin

if StrGrd.Col <i+1 then

StrGrd.ColCount:=StrGrd.ColCount+1;

if(not(SetGaussNumber(FloatToStr(StrToFloat(Frm.Edt_Average.Text)+RandG(0 ,1)*Power(StrToFloat(Frm.Edt_Dispersion.Text),1./2))))) then //StrToFloat(Frm.Edt_Average.Text) ,StrToFloat(Frm.Edt_Dispersion.Text )

begin

StrGrd.Cells[i+1,0]:='x'+IntToStr(i+1);

StrGrd.Cells[i+1,1]:=FloatToStr(StrToFloat(Frm.Edt_Average.Text)+RandG(0 ,1)*Power(StrToFloat(Frm.Edt_Dispersion.Text),1./2));

StrGrd.Cells[i+1,2]:='1';

end;

end;

end;

procedure TFrm.Edt_AverageChange(Sender: TObject);

begin

RdB_CompGenerate.Checked:=false;

RdB_CompGenerate.Checked:=true;

end;

procedure TFrm.Edt_DispersionChange(Sender: TObject);

begin

RdB_CompGenerate.Checked:=false;

RdB_CompGenerate.Checked:=true;

end;

end.

Додаток C. Результати виконання програми

Результати одержані при ручному вводі:

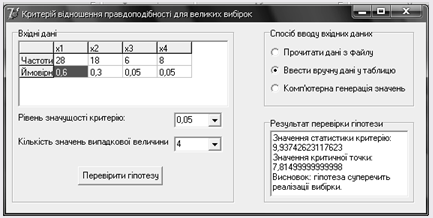
Результати отримані при зчитуванні з файлу:

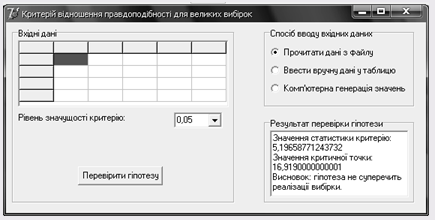
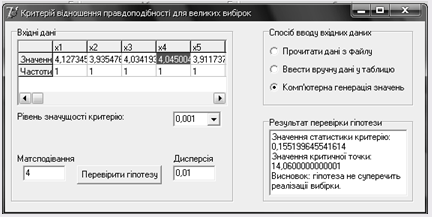
Дані згенеровані комп’ютером: