Курсовая работа: Моделирование рассеяния плоской упругой продольной волны на упругом однородном изотропном цилиндрическом слое

Курсовая работа: Моделирование рассеяния плоской упругой продольной волны на упругом однородном изотропном цилиндрическом слое

РЕФЕРАТ

Цель работы: моделирование рассеяния плоской упругой продольной волны на упругом однородном изотропном цилиндрическом слое.

Объем работы: 36 стр., в том числе таблиц - 1, приложений - 2.

Количество использованных источников: 16.

Ключевые слова: динамическая теория упругости,

упругая продольная волна,

упругий однородный изотропный слой,

краевая задача,

диаграмма рассеяния.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1. УРАВНЕНИЯ ВОЛНОВЫХ ПОЛЕЙ В УПРУГИХ ТЕЛАХ

1.1 Распространение упругих волн в однородных изотропных средах

1.2 Граничные условия

2. РАССЕЯНИЕ ПЛОСКОЙ ПРОДОЛЬНОЙ УПРУГОЙ ВОЛНЫ ОДНОРОДНЫМ ИЗОТРОПНЫМ ЦИЛИНДРИЧЕСКИМ СЛОЕМ

2.1 Постановка задачи

2.2 Рассеяние продольной волны

3. ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ И АНАЛИЗ РЕЗУЛЬТАТОВ

3.1 Постановка задачи

3.2 Численная реализация

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

ПРИЛОЖЕНИЕ 1. ЛИСТИНГ ПРОГРАММЫ

ПРИЛОЖЕНИЕ 2. ДИАГРАММЫ НАПРАВЛЕННОСТИ РАССЕЯННОГО ПОЛЯ

ВВЕДЕНИЕ

Акустические методы довольно широко применяются в исследовательской производственной практике. Традиционными областями их приложения являются сейсмология, геофизика, дефектоскопия и методы идентификации материалов. Теоретической основой практических технологий являются результаты исследований и математические модели распространения, дифракции и отражения звуковых и упругих волн.

В данной работе исследуется задача о рассеянии упругой волны на однородном цилиндрическом слое конечной толщины с бесконечной образующей.

Целью этой работы является получение выражения для рассеянного поля, в том числе в бесконечности, а также получение выражений для падающей, отраженной, прошедшей волны, найти волновое поле внутри неоднородного цилиндрического слоя.

В работе применяется метод сведения общих уравнений теории упругости к системе линейных алгебраических уравнений и ее разрешение методом Гаусса с выбором главного элемента. Построенные на основе полученных решений алгоритмы расчета характеристик прохождения и рассеяния упругих волн реализованы на ЭВМ в виде прикладной программы.

Результаты исследований могут быть использованы в сейсмологии, геофизике, дефектоскопии, методах идентификации материалов.

1. УРАВНЕНИЯ ВОЛНОВЫХ ПОЛЕЙ В УПРУГИХ ТЕЛАХ

1.1 Распространение упругих волн в однородных изотропных средах

Рассмотрим отдельно случай однородной упругой изотропной среды. В этом случае для цилиндрической системы координат мы получаем следующий закон Гука:

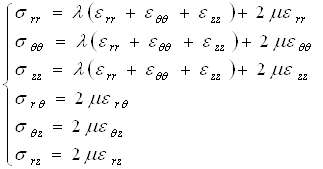, (1.1)

а уравнения движения Ламе:

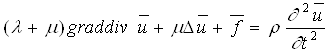 (1.2)

где  - оператор Лапласа:

 (1.3)

Отметим, что уравнения (1.2) записаны в векторной форме и, следовательно, справедливы в любой системе координат,

В однородной изотропной среде существует два типа волн; один из типов волн носит название волн сжатия-разрежения (или продольные волны), другой – волн сдвига (или поперечные волны). Относительно этих волн можно сказать, что они характеризуются различными скоростями распространения фронта, а также тем, что в волнах сжатия – разрежения отсутствует вращение частиц, а сдвиговые волны не сопровождаются изменением объема. Далее, если в некоторый момент волновое поле имеет продольный характер, то оно остается продольным всегда, то есть продольные волны в изотропной однородной безграничной среде при своем распространении не генерируют поперечных. В свою очередь поперечные волны, распространяясь в безграничной среде, не генерируют продольных волн. В однородной среде с границей продольные и поперечные волны распространяются независимо лишь то того момента, пока фронт не пересечет границу. Тогда образуются так называемые отраженные волны обоих типов, так как обычно системе граничных условий нельзя удовлетворить, введя отраженную волну какого-либо одного типа. Характер волны не меняется только в случае перпендикулярного падения волны на поверхность раздела и в случае падения под произвольным углом поперечной волны с параллельными плоскости раздела колебаниями.

Проведем в общем случае разделение произвольной упругой волны в неограниченном однородном изотропном пространстве на две независимо распространяющиеся с разными скоростями продольную и поперечную части.

Уравнение движения упругой изотропной среды без учета массовых сил имеет вид:

 

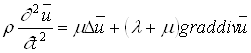
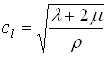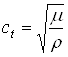Перепишем его, введя в него скорости  и  , которые представляют соответственно продольную и поперечную скорости распространения волны:

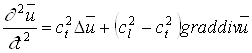 (1.4)

Представим вектор  в виде суммы двух частей: , одна из которых удовлетворяет условию , а другая - условию . Из векторного анализа известно, что такое представление всегда возможно (это есть представление вектора в виде суммы ротора некоторого вектора и градиента некоторого скаляра). При подстановке  в (1.4) получаем:

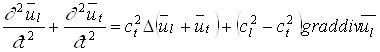 (1.5)

Применим к обеим сторонам этого уравнения операцию div. Поскольку , мы получим :

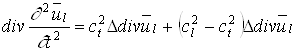
или

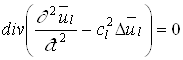
С другой стороны, так как , то rot стоящего в скобках выражения также равен нулю. Но если rot и div некоторого вектора исчезают во всем пространстве, то этот вектор тождественно равен нулю. Таким образом,

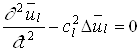 (1.6)

Аналогично применяя к уравнению (1.5) операцию rot и помня, что  и что rot всякого градиента равен нулю, находим

.

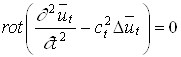Поскольку div стоящего в скобках выражения также равна нулю, то мы приходим к уравнению, подобному (1.6):

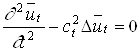 (1.7)

Уравнения (1.6), (1.7) представляют собой обычные волновые уравнения (в трех измерениях). Каждое из них соответствует распространению упругой волны со скоростью соответственно  или . Одна из этих волн не связана с изменением объема (в силу ), а другая  сопровождается объемными сжатиями и расширениями.

В упругой монохроматической волне вектор смещения имеет вид:

, (1.8)

где  - функция координат. Эта функция удовлетворяет уравнению

,

получающемуся при подстановке (1.8) в (1.4). Продольная и поперечная части монохроматической волны удовлетворяют уравнениям Гельмгольца:

,  (1.9)

где 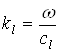, 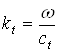- волновые векторы продольной и поперечной волн.

Пусть , а , где - скалярная функция, - векторная функция (соответственно скалярный и векторный потенциалы смещений, или продольный и поперечный потенциалы).

Покажем, что функции  и  удовлетворяют уравнениям Гельмгольца. Для этого подставим в уравнение движения упругой среды (1.4) вектор , и, изменяя порядок дифференцирования, получим:

 

Видно, что уравнение будет удовлетворяться, если положить:

,

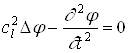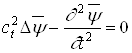
Если мы будем рассматривать зависимость от времени t у функций  и  как , то мы получаем уравнения Гельмгольца:

Произвольную плоскую волну можно разложить в спектр, то есть можно ее представить в виде суперпозиции плоских же гармонических волн. Поэтому имеет смысл изучать распространение гармонических волн. Зависимость от координат x,y в декартовой системе координат и времени t мы будем брать в виде экспоненты. Этот же результат можно получить, если применить к уравнениям Гельмгольца для потенциалов, записанным в декартовой системе координат, метод разделения переменных.

1.2 Граничные условия

Рассмотрим граничные условия на границе раздела сред при распространении упругой волны. Они заключаются в непрерывности компонент вектора смещения и непрерывности нормального  и касательных ,  компонент тензора напряжений при переходе через границу раздела сред.

В изотропной среде компоненты тензора напряжений  связаны с компонентами тензора деформаций  при помощи закона Гука (1.6), а компоненты тензора деформаций  связаны с компонентами вектора смещений  с помощью формулы (1.3). Рассмотрим цилиндрическую границу в цилиндрической системе координат. Если систему прямоугольных координат  выбрать таким образом, что ось z является осью цилиндра, то компоненты тензора напряжений выразятся через компоненты вектора смещения по формулам:

, (1.10)

где - нормальная компонента тензора напряжений,  - касательные компоненты,  и  - упругие константы Ламе.

2. РАССЕЯНИЕ ПЛОСКОЙ ПРОДОЛЬНОЙ УПРУГОЙ ВОЛНЫ ОДНОРОДНЫМ ИЗОТРОПНЫМ ЦИЛИНДРИЧЕСКИМ СЛОЕМ

2.1 Постановка задачи

Рассмотрим бесконечный изотропный полый круговой цилиндр с внешним радиусом  и внутренним - , модули упругости и плотность материала которого  . Цилиндрическая система координат  выбрана таким образом, что координатная ось z является осью вращения цилиндра. Будем считать, что окружающее и находящееся в полости упругие среды являются изотропными и однородными, имеющими плотности  и модули упругости ,  соответственно.

Пусть из полупространства  на упругий цилиндрический слой параллельно оси Ох в плоскости Оxy падает плоская упругая монохроматическая волна:

Определим отраженную от слоя и прошедшую через слой волны, а также найдем поле смещений внутри упругого слоя.

Фронт падающей волны перпендикулярен образующим цилиндра и поэтому задача является плоской, то есть смещения не зависят от координаты z.

Учтем, что в формуле , представляющей собой общее выражение для смещения, потенциал  в силу выбранной системы координат мы выбрали так, чтобы единственной отличной от нуля была компонента . Поэтому в силу линейности задачи мы можем рассматривать отдельно падение продольной волны , сдвиговой волны , где .

Мы осстановимся на рассмотрении рассеяния плоской продольной волны, представленной вектором падения: .

2.2 Рассеяние продольной волны

Пусть из внешнего пространства на упругий цилиндр перпендикулярно падает плоская упругая продольная волна, потенциал смещений которой равен:

,

где - волновой вектор,  - радиус-вектор,  - круговая частота. В дальнейшем временную зависимость  для простоты формул опускаем. В цилиндрической системе координат падающая волна может быть представлена в виде:

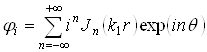, (2.1)

где - волновое число равное модулю вектора , , 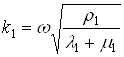- цилиндрическая функция Бесселя порядка n.

Определим отраженную от цилиндра и возбужденную в полости волны, а также найдем потенциалы смещений внутри слоя.

Вектор смещения в однородных изотропных средах также будет иметь всего две отличные от нуля компоненты:

 

Отраженная, возбужденная упругие волны, а также волны внутри однородного слоя являются решениями уравнений Гельмгольца. Причем их потенциалы также удовлетворяют уравнениям Гельмгольца и не зависят от координаты z. Следует иметь в виду, что вектор-функция  будет иметь лишь одну отличную от нуля компоненту , то есть .

Отраженная волна должна удовлетворять условиям излучения на бесконечности:

, (2.2)

а прошедшая волна – условию ограниченности. Поэтому потенциалы смещений этих волн будем искать в виде:

- для отраженной волны:

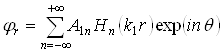, (2.3)

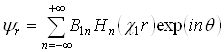
- для возбужденной волны:

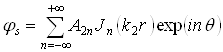, (2.4)

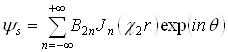
- для волны внутри слоя:

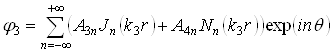 (2.5)

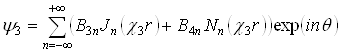
где 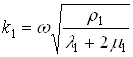, , 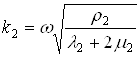, , 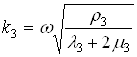, 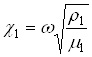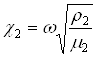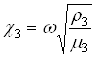- волновые числа.

Заметим, что представления (2.3) - (2.5) можно получить, применив метод разделения переменных к уравнениям Гельмгольца для потенциалов в цилиндрической системе координат от двух переменных. Мы получим функции вида:

.

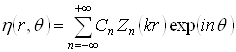Для того, чтобы потенциал отраженной волны удовлетворял условию излучения на бесконечности, необходимо в качестве цилиндрической функции Бесселя  выбрать цилиндрическую функцию Ханкеля первого рода , в этом случае потенциалу соответствует расходящейся волне с учетом того, что временной множитель выбран в виде . Для того, чтобы потенциал прошедшей волны удовлетворял условию ограниченности, необходимо в качестве цилиндрической функции Бесселя  выбрать цилиндрическую функцию Бесселя первого рода .  - цилиндрическая функция Неймана.

Коэффициенты подлежат определению из граничных условий, которые заключаются в непрерывности смещений и напряжений на обеих поверхностях упругого слоя. Имеем:

при : , , , ;

при : , , , ; (2.6)

где - компоненты вектора смещения частиц,  - компоненты тензора напряжений в средах  (j=1) ,  (j=2),  (j=3) соответственно.

Компоненты вектора смещения  связаны с потенциалами смещений следующим образом:

 (2.7)

Подставим (2.7) в (1.10), получим:

С учетом того, что дифференцирование по  - это умножение на , перепишем наши формулы:

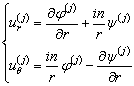 и

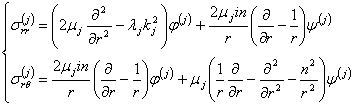
Подставим полученные выражения в граничные условия (2.6). В результате получим систему линейных алгебраических уравнений для коэффициентов :

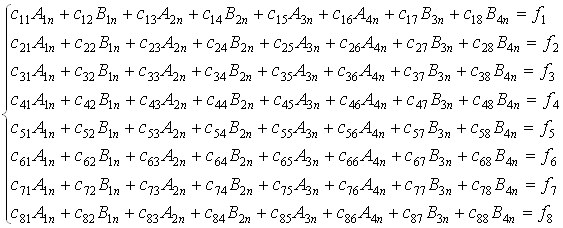
Разрешая для каждого n полученную систему одним из численных методов и подставляя полученные коэффициенты в потенциалы, найдем волновое поле, в том числе и в бесконечности.

Проведя вычисления для достаточно большого числа n, получаем возможность анализировать волновые поля вне и внутри оболочки по разложениям (2.2), (2.4), (2.5). В частности можно оценить поведение рассеянного поля в дальней зоне. Пользуясь асимптотическим представлением функций Ханкеля при больших значениях аргумента, для потенциала рассеянной продольной волны при  получим:

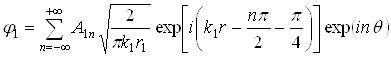
или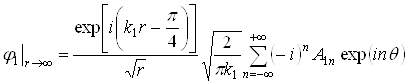

Опуская первый множитель, характеризующий распространение ненаправленной цилиндрической волны, и учитывая, что амплитуда падающей волны – единичная, получим выражение для нормированной амплитуды рассеянной волны:

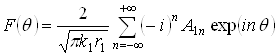 (2.8)

Это выражение определяет диаграмму направленности рассеянного поля по амплитуде.

3. ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ И АНАЛИЗ РЕЗУЛЬТАТОВ

3.1 Расчетные данные

Расчет будем проводить с материалами, модули упругости и плотность которых представлены в следующей таблице:

Таблица 1. Модули упругости и плотность материалов.

Материал И его тип
Изотропный (алюминий)	5.3	2.6	2.7
Изотропный (сталь)	11.2	8.1	7.7

Мы будем рассматривать алюминиевый цилиндрический слой, помещенный в упругое однородное изотропное пространство (сталь). Необходимые данные будут взяты из таблицы 1. Расчеты будем проводить при значениях радиусов: , , и при следующих частотах: =2.0, =3.0, = 4.0 (соответственно при количестве членов в ряде N=7.0, N=9.0, N=11.0).

3.2 Численная реализация

Алгоритм численного расчета реализован в виде программы kurs_ira.cpp на IBM – совместимых компьютерах на языке C++ в среде Borland версии 3.1. В качестве метода решения системы линейных алгебраических уравнений применялся метод Гаусса с выбором главного элемента. Листинг программы представлен в ПРИЛОЖЕНИИ 1. В качестве начальных данных в программе задаются плотности и модули упругости для различных сред, значения радиусов, номер задачи. В качестве результатов были получены диаграммы направленности рассеянного поля по амплитуде, представленные в ПРИЛОЖЕНИИ 2.

ЗАКЛЮЧЕНИЕ

В результате проделанной работы проделано следующее:

1.  Приведены волновые уравнения в изотропных однородных средах.

2.  Для однородной изотропной среды теоретически было показано разделение волны на продольную и поперечную части и приведены формулы для граничных условий.

3.  Поставлена и решена задача о прохождении плоской упругой продольной волны через упругий однородный изотропный цилиндрический слой и приведены диаграммы направленности рассеяния продольной волны по амплитуде. Листинг программы представлен в ПРИЛОЖЕНИИ 1. Расчетные данные взяты из таблицы 1.

4.  В качестве численного метода решения системы линейных алгебраических уравнений использован метод Гаусса с выбором главного элемента.

5.  В качестве результатов были получены графики диаграмм рассеянного поля продольной волны по амплитуде в ПРИЛОЖЕНИИ 2.

Эти результаты могут широко использоваться как в самой теории упругости, так и в ее приложениях в области дефектоскопии, геофизики, методах идентификации материалов.

ЛИТЕРАТУРА

1. Амензаде Ю.А. Теория упругости.- М.: Высшая школа, 1976, 272с.

2. Бреховских Л.М. Волны в слоистых средах.-М.: Изд-во АН СССР, 1957, 520c.

3. Гузь А.Н., Головчан В.Т. Дифракция упругих волн в многосвязных телах. – Киев, Наукова думка, 1972, 256с.

4. Исраилов М.Ш. Динамическая теория упругости и дифракции волн - М.: Изд-во МГУ, 1922, 205c.

5. Ландау Л.Д., Лившиц Е.М. Теория упругости.- М.: Наука, 1987, 248c.

6. Лехницкий С.Г. Теория упругости анизотропного тела.– М.:Наука,1977, 415с.

7. Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. - М.: Наука, 1966, 707с.

8. Новацкий В. Теория упругости. – М.: Мир, 1975. 872с.

9. Поручиков В.Б. Методы динамической теории упругости. – М.: Наука, 1986, 328c.

10. Рамская Е.И. Анализ собственных частот и форм осесимметричных колебаний трансверсально-изотропной полой сферы. // Прикладная механика, 1983, т. 19, N 7, c.103-107.

11. Скобельцын С.А., Толоконников Л.А. Прохождение звуковых волн через трансверсально–изотропный неоднородный плоский слой. // Акуст. журн., 1990, т.36, N4, с. 740-744.

12. Толоконников Л.А. Прохождение звука через неоднородный анизотропный слой, граничащий с вязкими жидкостями. // Прикладная математика и механика, 1998, т. 62, N 6, с. 1029-1035.

13. Шендеров Е.Л. Импедансы колебаний трансверсально-изотропного сферического слоя.// Акуст. журн., 1985, т. 31, N 5, с. 644-649.

14. Шендеров Е.Л. Шоренко И.Н. Импедансы колебаний изотропной и трансверсально-изотропной сферических оболочек, вычисленные по различным теориям.// Акуст. журн., 1986, т. 32, N 1, с. 101-106.

15. Шульга Н.А. Распространение осесимметричных упругих волн в ортотропном полом цилиндре.// Прикладная механика,1974,т.10,N9,c.14-18.

16. Шульга Н.А. Собственные колебания трансверсально-изотропной полой сферы.// Прикладная механика, 1980, т.16, N 12, c.108-110.

ПРИЛОЖЕНИЕ 1. ЛИСТИНГ ПРОГРАММЫ

#include<stdio.h>

#include<conio.h>

#include<complex.h>

#include<stdlib.h>

#include<graphics.h>

#define K 7

#define M 50

#define N 16

#define MM 8

complex iii=complex(0.0,1.0);

double w;

complex const_w;

double r1,r2,h=0.5,L1,L2,L3,M1,M2,M3,R1,R2,R3;

int zad;

double eps=0.000001;

double C=0.577215664901532;

double module(complex x)

{ return(sqrt(real(x)*real(x)+imag(x)*imag(x))); }

double fact(double n)

{

double i,k;

k=1.0;

for(i=1.0;i<(n+1.0);i++)

k=k*i;

return(k);

}

complex J(double x,double n)

{

double sum,s;

double k;

if(n<0.0) return(pow(-1.0,-n)*J(x,-n));

else

{

if(n>1.0) return(2.0*(n-1.0)/x*J(x,n-1.0)-J(x,n-2.0));

if(n==0.0)

{

          n=0.0;

          k=-1.0;

          sum=0.0;

          s=0.0;

          do{

           k=k+1.0;

           sum=sum+s;

           s=pow(-1.0,k)/fact(k)/fact(n+k)*pow(x/2.0,2*k+n);

           }while(module(s)>=eps);

          return(sum);

}

if(n==1.0)

{

          n=1.0;

          k=-1.0;

          sum=0.0;

          s=0.0;

          do{

           k=k+1.0;

           sum=sum+s;

           s=pow(-1.0,k)/fact(k)/fact(n+k)*pow(x/2.0,2*k+n);

           }while(module(s)>=eps);

          return(sum);

}

}

}

complex J_der(double x,double n)

{ return((J(x,n-1.0)-J(x,n+1.0))/2.0); }

complex J_der_der(double x,double n)

{ return((J_der(x,n-1.0)-J_der(x,n+1.0))/2.0); }

complex Ne(double x,double n)

{

complex sum1,sum2,sum3,s,ss,sss;

double k,nn,i;

if(n<0.0) return(pow(-1.0,-n)*Ne(x,-n));

else

{

if(n>1.0) return(2.0*(n-1.0)/x*Ne(x,n-1.0)-Ne(x,n-2.0));

if(n==0.0)

{

          n=0.0;

          sum1=2.0/M_PI*(C+log(x/2.0))*J(x,n);

          sum2=0.0;

          for(k=0.0;k<n;k=k+1.0)

           sum2=sum2+fact(n-k-1.0)/fact(k)*pow(x/2.0,2.0*k-n);

          sum2=-sum2/M_PI;

          k=-1.0;

          sum3=0.0;

          s=0.0;

          do{

           k=k+1.0;

           sum3=sum3+s;

           s=pow(-1.0,k)/fact(k)/fact(n+k)*pow(x/2.0,2*k+n);

           ss=0.0;

           for(i=0.0;i<(k+1.0);i=i+1.0)

           {

           sss=0.0;

           for(nn=1.0;nn<(n+i+1.0);nn=nn+1.0)

                   sss=sss+1.0/nn;

           ss=ss+sss;

           }

           s=s*ss;

           }while(module(s)>=eps);

          sum3=-sum3/M_PI;

          return(sum1+sum2+sum3);

}

if(n==1.0)

{

          n=1.0;

          sum1=2.0/M_PI*(C+log(x/2.0))*J(x,n);

          sum2=0.0;

          for(k=0.0;k<n;k=k+1.0)

           sum2=sum2+fact(n-k-1.0)/fact(k)*pow(x/2.0,2.0*k-n);

          sum2=-sum2/M_PI;

          k=-1.0;

          sum3=0.0;

          s=0.0;

          do{

           k=k+1.0;

           sum3=sum3+s;

           s=pow(-1.0,k)/fact(k)/fact(n+k)*pow(x/2.0,2*k+n);

           ss=0.0;

           for(i=0.0;i<(k+1.0);i=i+1.0)

           {

           sss=0.0;

           for(nn=1.0;nn<(n+i+1.0);nn=nn+1.0)

                   sss=sss+1.0/nn;

           ss=ss+sss;

           }

           s=s*ss;

           }while(module(s)>=eps);

          sum3=-sum3/M_PI;

          return(sum1+sum2+sum3);

}

}

}

complex Ne_der(double x,double n)

{ return((Ne(x,n-1.0)-Ne(x,n+1.0))/2.0); }

complex Ne_der_der(double x,double n)

{ return((Ne_der(x,n-1.0)-Ne_der(x,n+1.0))/2.0); }

complex H1(double x,double n)

{ return(J(x,n)+iii*Ne(x,n)); }

complex H1_der(double x,double n)

{ return(J_der(x,n)+iii*Ne_der(x,n)); }

complex H1_der_der(double x,double n)

{ return(J_der_der(x,n)+iii*Ne_der_der(x,n)); }

void mod_upr(void)

{

if(zad==1)

{

L1=11.2*pow(10.0,11.0);

M1=8.1*pow(10.0,11.0);

R1=7.7;

L3=5.3*pow(10.0,11.0);

M3=2.6*pow(10.0,11.0);

R3=2.7;

L2=11.2*pow(10.0,11.0);

M2=8.1*pow(10.0,11.0);

R2=7.7;

}

if(zad==2)

{

L1=5.3*pow(10.0,11.0);

M1=2.6*pow(10.0,11.0);

R1=2.7;

L3=11.2*pow(10.0,11.0);

M3=8.1*pow(10.0,11.0);

R3=7.7;

L2=5.3*pow(10.0,11.0);

M2=2.6*pow(10.0,11.0);

R2=2.7;

}

}

double k1,xi1,k2,xi2,k3,xi3;

complex A1_n[K+K+2],A2_n[K+K+2],A3_n[K+K+2],A4_n[K+K+2];

complex B1_n[K+K+2],B2_n[K+K+2],B3_n[K+K+2],B4_n[K+K+2];

complex A[MM][MM];

complex F[MM];

complex X[MM];

float a[N][N];

float f[N];

float x[N];

void Matrix_A_F(float n)

{

A[0][0]=k1*H1_der(k1*r1,n);

A[0][1]=iii*n/r1*H1(xi1*r1,n);

A[0][2]=0.0;

A[0][3]=0.0;

A[0][4]=-k3*J_der(k3*r1,n);

A[0][5]=-k3*Ne_der(k3*r1,n);

A[0][6]=-iii*n/r1*J(xi3*r1,n);

A[0][7]=-iii*n/r1*Ne(xi3*r1,n);

F[0]=-pow(iii,n)*k1*J_der(k1*r1,n);

A[1][0]=0.0;

A[1][1]=0.0;

A[1][2]=k2*J_der(k2*r2,n);

A[1][3]=iii*n/r2*J(xi2*r2,n);

A[1][4]=-k3*J_der(k3*r2,n);

A[1][5]=-k3*Ne_der(k3*r2,n);

A[1][6]=-iii*n/r2*J(xi3*r2,n);

A[1][7]=-iii*n/r2*Ne(xi3*r2,n);

F[1]=0.0;

A[2][0]=iii*n/r1*H1(k1*r1,n);

A[2][1]=-xi1*H1_der(xi1*r1,n);

A[2][2]=0.0;

A[2][3]=0.0;

A[2][4]=-iii*n/r1*J(k3*r1,n);

A[2][5]=-iii*n/r1*Ne(k3*r1,n);

A[2][6]=xi1*J_der(xi3*r1,n);

A[2][7]=xi3*Ne_der(xi3*r1,n);

F[2]=-pow(iii,n+1.0)*n/r1*J(k1*r1,n);

A[3][0]=0.0;

A[3][1]=0.0;

A[3][2]=iii*n/r2*J(k2*r2,n);

A[3][3]=-xi2*J_der(xi2*r2,n);

A[3][4]=-iii*n/r2*J(k3*r2,n);

A[3][5]=-iii*n/r2*Ne(k3*r2,n);

A[3][6]=xi3*J_der(xi3*r2,n);

A[3][7]=xi3*Ne_der(xi3*r2,n);

F[3]=0.0;

A[4][0]=2.0*M1*k1*k1*H1_der_der(k1*r1,n)-L1*k1*k1*H1(k1*r1,n);

A[4][1]=2.0*M1*iii*n/r1*(xi1*H1_der(xi1*r1,n)-H1(xi1*r1,n)/r1);

A[4][2]=0.0;

A[4][3]=0.0;

A[4][4]=-2.0*M3*k3*k3*J_der_der(k3*r1,n)-L3*k3*k3*J(k3*r1,n);

A[4][5]=-2.0*M3*k3*k3*Ne_der_der(k3*r1,n)-L3*k3*k3*Ne(k3*r1,n);

A[4][6]=-2.0*M3*iii*n/r1*(xi3*J_der(xi3*r1,n)-J(xi3*r1,n)/r1);

A[4][7]=-2.0*M3*iii*n/r1*(xi3*Ne_der(xi3*r1,n)-Ne(xi3*r1,n)/r1);

F[4]=-pow(iii,n)*(2.0*M1*k1*k1*J_der_der(k1*r1,n)-L1*k1*k1*J(k1*r1,n));

A[5][0]=2.0*M1*iii*n/r1*(k1*H1_der(k1*r1,n)-H1(k1*r1,n)/r1);

A[5][1]=M1*(-xi1*xi1*H1_der_der(xi1*r1,n)-n*n/r1/r1*H1(xi1*r1,n)+xi1/r1*H1_der(xi1*r1,n));

A[5][2]=0.0;

A[5][3]=0.0;

A[5][4]=-2.0*M3*iii*n/r1*(k3*J_der(k3*r1,n)-J(k3*r1,n)/r1);

A[5][5]=-2.0*M3*iii*n/r1*(k3*Ne_der(k3*r1,n)-Ne(k3*r1,n)/r1);

A[5][6]=-M3*(-xi3*xi3*J_der_der(xi3*r1,n)-n*n/r1/r1*J(xi3*r1,n)+xi3/r1*J_der(xi3*r1,n));

A[5][7]=-M3*(-xi3*xi3*Ne_der_der(xi3*r1,n)-n*n/r1/r1*Ne(xi3*r1,n)+xi3/r1*Ne_der(xi3*r1,n));

F[5]=-2.0*M1/r1*pow(iii,n+1.0)*n*(k1*J_der(k1*r1,n)-J(k1*r1,n)/r1);

A[6][0]=0.0;

A[6][1]=0.0;

A[6][2]=2.0*M2*k2*k2*J_der_der(k2*r2,n)-L2*k2*k2*H1(k2*r2,n);

A[6][3]=2.0*M2*iii*n/r2*(xi2*H1_der(xi2*r2,n)-H1(xi2*r2,n)/r2);

A[6][4]=-2.0*M3*k3*k3*J_der_der(k3*r2,n)-L3*k3*k3*J(k3*r2,n);

A[6][5]=-2.0*M3*k3*k3*Ne_der_der(k3*r2,n)-L3*k3*k3*Ne(k3*r2,n);

A[6][6]=-2.0*M3*iii*n/r2*(xi3*J_der(xi3*r2,n)-J(xi3*r2,n)/r2);

A[6][7]=-2.0*M3*iii*n/r2*(xi3*Ne_der(xi3*r2,n)-Ne(xi3*r2,n)/r2);

F[6]=0.0;

A[7][0]=0.0;

A[7][1]=0.0;

A[7][2]=2.0*M2*iii*n/r2*(k2*H1_der(k2*r2,n)-H1(k2*r2,n)/r2);

A[7][3]=M2*(-xi2*xi2*H1_der_der(xi2*r2,n)-n*n/r2/r2*H1(xi2*r2,n)+xi2/r2*H1_der(xi2*r2,n));

A[7][4]=-2.0*M3*iii*n/r2*(k3*J_der(k3*r2,n)-J(k3*r2,n)/r2);

A[7][5]=-2.0*M3*iii*n/r2*(k3*Ne_der(k3*r2,n)-Ne(k3*r2,n)/r2);

A[7][6]=-M3*(-xi3*xi3*J_der_der(xi3*r2,n)-n*n/r2/r2*J(xi3*r2,n)+xi3/r2*J_der(xi3*r2,n));

A[7][7]=-M3*(-xi3*xi3*Ne_der_der(xi3*r2,n)-n*n/r2/r2*Ne(xi3*r2,n)+xi3/r2*Ne_der(xi3*r2,n));

F[7]=0.0;

}

void Real_Gauss(void)

{

int i,j,k,l,maxk;

float max,w[N],v[N][N],sum,e,c;

for(i=0;i<N;i++)

{

for(j=0;j<N;j++)

          v[i][j]=a[i][j];

w[i]=f[i];

}

for(k=0;k<N;k++)

{

maxk=k;

max=fabs(a[k][k]);

for(i=k;i<N;i++)

          if(fabs(a[i][k])>max)

           {

           maxk=i;

           max=fabs(a[i][k]);

           }

for(i=0;i<N;i++)

          {

           e=a[k][i];

           a[k][i]=a[maxk][i];

           a[maxk][i]=e;

          }

e=f[k];

f[k]=f[maxk];

f[maxk]=e;

for(i=k+1;i<N;i++)

          {

           c=a[i][k]/a[k][k];

           f[i]=f[i]-f[k]*c;

           for(j=k;j<N;j++)

           a[i][j]=a[i][j]-a[k][j]*c;

          }

}

for(i=0;i<N;i++)

x[i]=0.0;

for(i=N-1;i>=0;i--)

{

c=0.0;

for(j=i+1;j<N;j++)

          c=c+a[i][j]*x[j];

x[i]=(f[i]-c)/a[i][i];

}

}

void Complex_Gauss(void)

{

int i,j;

complex sum;

for(i=0;i<MM;i++)

{

a[2*i][0]=real(A[i][0]); a[2*i][1]=-imag(A[i][0]);

a[2*i][2]=real(A[i][1]); a[2*i][3]=-imag(A[i][1]);

a[2*i][4]=real(A[i][2]); a[2*i][5]=-imag(A[i][2]);

a[2*i][6]=real(A[i][3]); a[2*i][7]=-imag(A[i][3]);

a[2*i][8]=real(A[i][4]); a[2*i][9]=-imag(A[i][4]);

a[2*i][10]=real(A[i][5]); a[2*i][11]=-imag(A[i][5]);

a[2*i][12]=real(A[i][6]); a[2*i][13]=-imag(A[i][6]);

a[2*i][14]=real(A[i][7]); a[2*i][15]=-imag(A[i][7]);

          f[2*i]=real(F[i]);

a[2*i+1][0]=imag(A[i][0]); a[2*i+1][1]=real(A[i][0]);

a[2*i+1][2]=imag(A[i][1]); a[2*i+1][3]=real(A[i][1]);

a[2*i+1][4]=imag(A[i][2]); a[2*i+1][5]=real(A[i][2]);

a[2*i+1][6]=imag(A[i][3]); a[2*i+1][7]=real(A[i][3]);

a[2*i+1][8]=imag(A[i][4]); a[2*i+1][9]=real(A[i][4]);

a[2*i+1][10]=imag(A[i][5]); a[2*i+1][11]=real(A[i][5]);

a[2*i+1][12]=imag(A[i][6]); a[2*i+1][13]=real(A[i][6]);

a[2*i+1][14]=imag(A[i][7]); a[2*i+1][15]=real(A[i][7]);

          f[2*i+1]=imag(F[i]);

}

Real_Gauss();

X[0]=complex(x[0],x[1]);

X[1]=complex(x[2],x[3]);

X[2]=complex(x[4],x[5]);

X[3]=complex(x[6],x[7]);

X[4]=complex(x[8],x[9]);

X[5]=complex(x[10],x[11]);

X[6]=complex(x[12],x[13]);

X[7]=complex(x[14],x[15]);

}

void grafic(double *k_1, double *k_2, double *k_3, double *k_4, double a, double b, double c, double d, double col_x, double col_y)

{

double h,hx,hy,dx,dy;

int i,maxx,maxy;

int borderx_left=0,borderx_right=0;

int bordery_up=0,bordery_down=0;

int gdriver=DETECT, gmode, errorcode;

clrscr();

initgraph(&gdriver,&gmode," ");

errorcode=graphresult();

if(errorcode!=grOk)

{

printf("Не могу открыть графический экран!\n");

printf("Нажмите любую клавишу!\n");

getch();

exit(1);

}

setfillstyle(SOLID_FILL,WHITE);

floodfill(0,0,WHITE);

maxx=getmaxx();

maxy=getmaxy();

h=(double)(maxx-(borderx_left+borderx_right));

hx=(b-a)/h;

h=(double)(maxy-(bordery_up+bordery_down));

hy=(d-c)/h;

setcolor(BLACK);

line(borderx_left,bordery_up,borderx_left,maxy-bordery_down);

line(borderx_left,maxy-bordery_down,maxx-borderx_right,maxy-bordery_down);

line(maxx-borderx_right,maxy-bordery_down,maxx-borderx_right,bordery_up);

line(maxx-borderx_right,bordery_up,borderx_left,bordery_up);

line(0,0,0,maxy);

line(0,maxy,maxx,maxy);

line(maxx,maxy,maxx,0);

line(maxx,0,0,0);

dx=(b-a)/col_x;

dy=(d-c)/col_y;

setcolor(BLACK);

for(i=1;i<col_x;i++)

line(borderx_left+i*dx/hx,bordery_up,borderx_left+i*dx/hx,maxy-bordery_down);

for(i=1;i<col_y;i++)

line(borderx_left,bordery_up+i*dy/hy,maxx-borderx_right,bordery_up+i*dy/hy);

setcolor(BLACK);

for(i=0;i<M;i++)

line(borderx_left+(k_1[i]-a)/hx, maxy-bordery_down-(k_2[i]-c)/hy,

           borderx_left+(k_1[i+1]-a)/hx, maxy-bordery_down-(k_2[i+1]-c)/hy);

setcolor(BLACK);

for(i=0;i<M;i++)

line(borderx_left+(k_3[i]-a)/hx, maxy-bordery_down-(k_4[i]-c)/hy,

           borderx_left+(k_3[i+1]-a)/hx, maxy-bordery_down-(k_4[i+1]-c)/hy);

getch();

closegraph();

}

double F_rass(double fi)

{

complex sum;

int i;

sum=0.0;

for(i=-K;i<=K;i=i+1.0)

sum=sum+pow(iii,i)*A1_n[K-i]*exp(iii*i*fi);

sum=2.0/sqrt(M_PI*const_w)*module(sum);

return(module(sum));

}

void main(void)

{

int j;

double k,n;

double k_0,k_n,dk;

double k_1[M+1],k_2[M+1],k_3[M+1],k_4[M+1];

clrscr();

const_w=2.0;

r1=3.5;

r2=1.0;

for(j=0;j<(M+1);j++)

{

k_1[j]=0.0;

k_2[j]=0.0;

k_3[j]=0.0;

k_4[j]=0.0;

}

clrscr();

k_0=M_PI;

k_n=2.0*M_PI;

dk=(k_n-k_0)/M;

j=0;

zad=1;

mod_upr();

w=module(const_w*sqrt((L1+2.0*M1)/R1)/(r1-r2));

k1=w/sqrt((L1+2.0*M1)/R1);

k2=w/sqrt((L2+2.0*M2)/R2);

k3=w/sqrt((L3+2.0*M3)/R3);

xi1=w/sqrt(M1/R1);

xi2=w/sqrt(M2/R2);

xi3=w/sqrt(M3/R3);

for(n=-K;n<=K;n=n+1)

{

Matrix_A_F(n);

Complex_Gauss();

A1_n[K-n]=X[0];

B1_n[K-n]=X[1];

A2_n[K-n]=X[2];

B2_n[K-n]=X[3];

A3_n[K-n]=X[4];

A4_n[K-n]=X[5];

B3_n[K-n]=X[6];

B4_n[K-n]=X[7];

}

for(j=0,k=k_0;k<=k_n;k=k+dk,j++)

{

k_1[j]=-F_rass(k)*cos(k);

k_2[j]=-F_rass(k)*sin(k);

k_3[j]=-F_rass(k)*cos(k);

k_4[j]=F_rass(k)*sin(k);

}

grafic(k_1,k_2,k_3,k_4,-2.0,6.0,-2.0,2.0,8.0,4.0);

}

ПРИЛОЖЕНИЕ 2

ДИАГРАММЫ РАССЕЯННОГО ПОЛЯ ПО АМПЛИТУДЕ

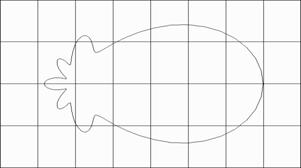
Алюминий (kr=2.0, N=7)

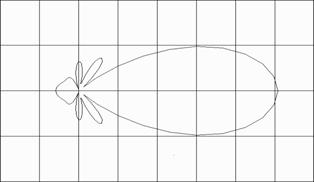
Алюминий (kr=3.0, N=9)

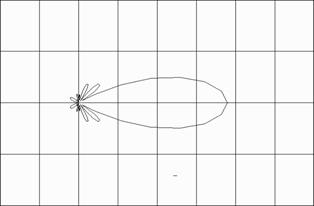
Алюминий (kr=4.0, N=11)