Реферат: Построение эйлерова цикла. Алгоритм Форда и Уоршелла

Реферат: Построение эйлерова цикла. Алгоритм Форда и Уоршелла

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра информатики

РЕФЕРАТ

на тему:

«Построение эйлерова цикла. Алгоритм форда и Уоршелла»

МИНСК, 2008

1. Эйлеровы цепи и циклы

Рассматриваемая задача является одной из самых ста­рей­ших в теории графов. В городе Кенигсберге (ныне Калининград) имелось семь мостов, соединяющих два берега реки Преголь, и два основа на ней друг с другом (рис. 1а). Требуется, начав путешествие из одной точки города прой­ти по всем мостам по одному разу и вернуться в исходную точку.

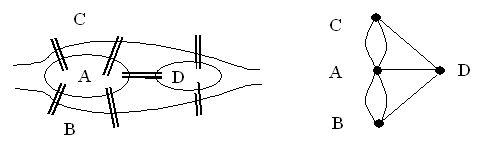
а)                                                       б)

Рис. 1.

Если поставить в соответствие мостам ребра, а участкам суши — вершины, то получится граф (точнее псевдограф), в котором надо найти про­стой цикл, проходящий через все ребра. В общем виде эта задача была решена Эйлером в 1736 г.

Определение 1. Эйлеровой цепью в неориентированном графе G называется простая цепь, содержащая все ребра графа G. Эйлеровым циклом назы­вается замкнутая Эйлерова цепь. Аналогично, эйлеров путь в орграфе G — это простой путь, содержащий все дуги графа G. Эйлеров контур в орграфе G — это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называется эйлеровым.

Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой.

Теорема 1. (Эйлер) Эйлеров цикл в связном неориентированном графе G(X, E) существует только тогда, когда все его вершины имеют четную степень.

Доказательство. Необходимость. Пусть m - эйлеров цикл в связном гра­фе G, x — произвольная вершина этого графа. Через вершину x эйлеров цикл проходит некоторое количество k (k³1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2k, т.е. четна, так как x выбрана произвольно, то все вершины в графе G имеют четную сте­пень.

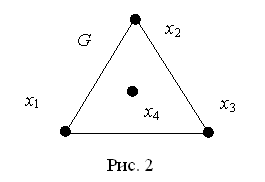
Достаточность. Воспользуемся индукцией по числу m ребер графа. Эйле­ровы циклы для обычных (не псевдо) графов можно построить начиная с m=3.Легко проверить, что единственный граф с m=3, имеющий все вершины с четными степенями, есть граф K3 (рис. 2). Существование эйлерова цикла в нем очевидно. Таким образом, для m=3 достаточность условий доказываемой теоремы имеет место. Пусть теперь граф G имеет m>3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чем m ребер. Зафиксируем произвольную вершину a графа G и будем искать простой цикл, идущий из a в a. Пусть m(a, x) — простая цепь, иду­щая из a в некоторую вершину x. Если x ¹ a, то цепь m можно продолжить из вершины x в некотором направлении. Через некоторое число таких про­дол­­же­ний мы придем в вершину zÎX, из которой нельзя продлить полу­чен­ную про­стую цепь. Легко видеть, что z = a так как из всех остальных вершин цепь может выйти (четные степени!); a в a она начиналась. Таким образом, нами построен цикл m, идущий из a в a. Предположим, что построенный про­стой цикл не содержит всех ребер графа G. Удалим ребра, входящие в цикл m, из графа G и рассмотрим полученный граф . В графе  все вершины имеют четные степени. Пусть  — компо­нен­ты связ­нос­ти графа , содержащие хотя бы по одному ребру. Соглас­но пред­поло­же­нию индукции все эти компоненты обладают эйлеровыми циклами m1, m1, …, mk соот­вет­ствен­но. Так как граф G связан, то цепь m встре­чает каждую из компонент. Пусть первые встречи цикла m с ком­понентами  происходят соответственно в вершинах x1, x2, …, xk. Тогда про­стая цепь

      n(a, a)=m(a, x1) U m1(x1, x1) U m(x1, x2) U…U mk(xk, xk) U m(xk, a)

является эйлеровым циклом в графе G. Теорема доказана.

Замечание. Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 1,а).

Таким образом, задача о кенигсбергских мостах не имеет ре­ше­ния, так как соответствующий граф (см. рис. 1,б) не имеет эйлерова цикла из-за не­четности степеней все вершин.

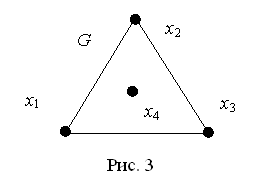Отметим, что из существования эйле­ро­ва цикла в неориентированном графе G не следует связность этого графа. Напри­мер, неориентированный граф G на рис. 3 обладает эйлеровым циклом и вместе с тем несвязен.

Совершенно также, как теорема 1, могут быть доказаны следующие два утверждения.

Теорема 2. Связный неориентированный граф G обладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом.

Теорема 3. Сильно связный орграф G(X, E) обладает эйлеровым кон­ту­ром тогда и только тогда, когда для любой вершины xÎX выполняется

                                               .

Можно также обобщить задачу, которую решал Эйлер следующим обра­зом. Будем говорить что множество не пересекающихся по ребрам простых цепей  графа G покрывает его, если все ребра графа G включены в цепи mi. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G.

Если граф G — эйлеров, то очевидно, что это число равно 1. Пусть теперь G не является эйлеровым графом. Обозначим через k число его вер­шин нечетной степени. По теореме … k четно. Очевидно, что каждая верши­на нечетной степени должна быть концом хотя бы одной из покрывающих G цепей mi. Следовательно, таких цепей будет не менее чем k/2. С другой сто­роны, таким количеством цепей граф G покрыть можно. Чтобы убедиться в этом, расширим G до нового графа , добавив k/2 ребер , соединяющих раз­личные пары вершин нечетной степени. Тогда  оказывается эйлеровым графом и имеет эйлеров цикл . После удаления из  ребер  граф разло­жится на k/2 цепей, покрывающих G. Таким образом, доказана.

Теорема 4. Пусть G — связный граф с k>0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающих G, равно k/2.

Алгоритм построения эйлерова цикла

Для начала отметим, что теорема 1 также дает метод построения эйлерова цикла. Здесь мы рассмотрим несколько иной алгоритм.

Пусть G(X, E) — связный неорентированный граф, не имеющий вершин нечетной степени. Назовем мостом такое ребро, удаление которого из связного графа разбивает этот граф на две компоненты связности, имеющие хотя бы по одному ребру.

1°. Пусть a — произвольная вершина графа G. Возьмем любое ребро e1=(a, x1) , инцидентное вершине a, и положим m = {e1}.

2°. Рассмотрим подграф G1(X, E\m1). Возьмем в качестве e2 ребро, инци­дентное вершине x1 и неинцидентное вершине a, которое также не является мостом в подграфе G1 (если такое ребро e2 существует!). Получим простую цепь m2 = {e1, e2}.

3°. Пусть e2 = (x1, x2), x ¹ a. Рассмотрим подграф G2(X, E\m2) и удалим из него все изо­лированные вер­шины. В полученном подграфе  выберем ребро e3ÎE\m2, инцидентное вершине a, которое не является мостом в под­графе  (если такое ребро e3 суще­ству­ет!). Получим простую цепь

                                           m3 = {e1, e2, e3}.

Продолжая указанный процесс, мы через конечное число шагов получим эйлеров цикл m = {e1, e2, …, en}, где n — число ребер графа G(X, E).

Обоснование алгоритма

Предположим, что уже построена простая цепь mk-1 = {e1, e2, …, ek-1} для k³2 методом, указанным в алгоритме. Пусть ek-1 = (xk-2, xk-1) и xk-1 ¹ a. Рас­смо­трим подграф , который получается из подграфа Gk-1(X, E\mk-1) удалением всех изолированных вершин. Вершина xk-1 в этом подграфе  имеет нечет­ную степень, поэтому существует по крайней мере одно ребро ekÎE\mk-1, ин­ци­дентное xk-1. Если это ребро единственное, то оно не является мостом в графе . В противном случае вершина a будет связана с некоторой вер­ши­ной  единственной цепью, содержащей ребро ek, что противоречит суще­ствованию эйлерова цикла в графе G. Поскольку ek - не мост, то процесс мож­но продолжать, взяв . Если ребро ek не единственное инци­дентное вершине xk-1, то среди этих ребер есть по крайней мере одно, не явля­ющееся мостом. В противном случае один из этих мостов  можно выбро­сить так, что вершины xk-1 и a попадут в разные компоненты связности графа . Если xk-1 принадлежит компоненте M, то в этой компоненте все вер­шины имеют четную степень, поэтому существует эйлеров цикл в M, про­хо­дящий через xk-1. Этот цикл содержит все ребра, инцидентные xk-1 и при­над­лежащие , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро ek, инцидентное вершине xk-1 и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв

                                          .

Из предыдущего следует, что процесс нельзя продолжать тогда и только тогда, когда мы попадем в вершину a, причем степень вершины a относительно непройденных ребер равна нулю. Докажем, что в этом случае построенный цикл m - простой цикл. Покажем, что m содержит все ребра графа G. Если не все ребра графа G принадлежат m, то не принадлежащие m ребра порождают компоненты связности C1, …, Cm (m³1) в подграфе . Пусть компонента Ci, 1£i£m соединяется с циклом m в вершине yi. Если существует ребро eÎm , такое, что e=(yi, a), то при построении цикла m было нарушено правило выбора ребра e, что невозможно. Если часть цикла m, соединяющая yi и a, состоит более чем из одного ребра, то первое ребро этой части  было мостом, и поэтому было нарушено правило вы­бора , что невозможно. Итак, непройденных ребер быть не может, поэ­тому m - эйлеров цикл.

2. НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ

Рассматрим ориентированные графы G(X, E) каждой дуге eÎE которого ставится в соответствие вещественное число l(e). Т.е. на множестве Е создана функция l:E®R. Такой граф принято называть нагруженным. Само число l называется весом дуги.

Можно увидеть аналогию между, например, картой автомобильных или железных дорог. Тогда множество вершин Х будет соответствовать городам, множество дуг – магистралям, соединяющим города, а веса – расстояниям. (На практике, при этом, фактически получится неориентированный граф).

В связи с изложенной аналогией будем называть веса дуг расстояниями.

Определение 2.1. Пусть имеется последовательность вершин x0, x1, …, xn, которая определяет путь в нагруженном графе G(X, E), тогда длина этого пути определяется как .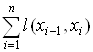

Естественный интерес представляет нахождение кратчайшего пути между двумя заданными вершинами x и y.

 

Алгоритм Форда отыскания кратчайшего пути.

Будем предполагать, что все расстояния в графе положительны. (Если это не так, то ко всем весам можно всегда добавить такую константу, что все эти веса станут положительными).

Пусть мы ищем путь от вершины x0 к вершине xn. Будем каждой вершине xi ставить в соответствие некоторое число li по следующим правилам.

1° Положим l0= 0, li = ¥ (достаточно большое число) для "i > 0.

2° Ищем в графе дугу (xi, xj) удовлетворяющую следующему условию

                                           lj - li > l(xi, xj),                                            (1)

после чего заменяем lj на

                                         .

Пункт 2° повторяется до тех пор, пока невозможно будет найти дугу, удовлетворяющую условию (1). Обоснуем этот алгоритм и укажем как определяется кратчайший путь.

Отметим, что ln монотонно уменьшается, то после завершения алгоритма найдется дуга , такая, что  для которой последний раз уменьшалось ln. (Иначе вообще нет пути между x0 и xn или для  верно (1)).

По этой же самой причине найдется вершина , такая , что

                                     ,

этот процесс может продолжаться и дальше, так что получится строго убыва­ю­щая последовательность  . Отсюда следует, что при некото­ром k мы получим .

Покажем, что  – минимальный путь с длиной ln, т.е. длина любого другого пути между x0 и xn не превышает kn.

Возьмем произвольный путь  и рассмотрим его длину .

После завершения алгоритма имеем следующие соотношения

                                     

Сложив все эти неравенства, получим

                                ,

что и требовалось доказать.

Рассмотрим пример.

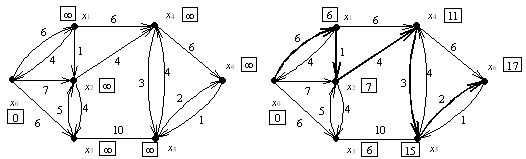а                                                               б

Рис. 2.1

На рис. 2.1а изображен исходный помеченный граф и начальные значения li. На рис. 2.1б для того же графа указаны конечные значения li и выделен кратчайший путь. Пометка вершин графа происходила в следующем порядке (в скобках указана дуга, вдоль которой выполняется (1)):

l1 = 6    (x0, x1),

l2 = 7    (x0, x2),

l3 = 6    (x0, x3),

l4 = 12   (x1, x3),

l4 = 11   (x2, x4),

l5 = 16   (x3, x4),

l5 = 15   (x4, x5),

l6 = 18   (x4, x6),

l6 = 17   (x5, x6).

Иногда возникает задача отыскания кратчайших расстояний между всеми парами вершин. Одним из способов решения этой задачи является

 

Алгоритм Флойда

Обозначим lij длину дуги (xi, xj), если таковой не существует примем lij = ¥, кроме того, положим lii = 0. Обозначим  длину кратчайшего из путей из xi в xj с промежуточными вершинами из множества {x1, …, xm}. Тогда можно получить следующие уравнения

                                                ,                                                 (2)

                               .                                 (3)

Уравнение (2) очевидно. Обоснуем уравнение (3). Рассмотрим кратчай­ший путь из xi в xj с промежуточными вершинами из множества {x1, …, xm, xm+1}. Если этот путь не содержит xm+1, то . Если же он содержит xm+1, то деля путь на отрезки от xi до xm+1 и от xm+1 до xj, получаем равенство .

Уравнения (2) и (3) позволяют легко вычислить матрицу расстояний [dij] между всеми парами вершин графа G(X, E). На первом этапе согласно (2) составляем n´n матрицу  равную матрице [lij] весов ребер (n – число вершин G(X, E)). n раз производим вычисление по итерационной формуле (3), после чего имеем  – матрицу расстояний.

Отметим, что алгоритм Флойда непосредственно не указывает сам кратчайший путь между вершинами, а только его длину. Алгоритм Флойда можно модифицировать таким образом, чтобы можно было находить и сами пути. Для этого получим вспомогательную матрицу [Rij], которая будет содержать наибольший номер вершины некоторого кратчайшего пути из xi в xj (Rij=0, если этот путь не содержит промежуточных вершин).

Эта матрица вычисляется параллельно с  по следующим правилам

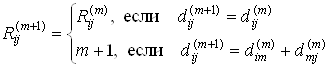
Последнее выражение следует из обоснования (3).

Теперь кратчайший путь выписывается из следующего рекурсивного алгоритма:

Кратчайший путь из xi в xj:

1°. Если Rij = 0    то выполнить 2°,

иначе выполнить 3°.

2°. Если i=j         то выписать xi и закончить,

иначе выписать xi и xj закончить.

3°. Выписать кратчайший путь между xi и .

4°. Выписать кратчайший путь между  и xj.

Пункты 3° и 4° предполагают рекурсивное обращение к рассмотренному алгоритму.

С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения.

Напомним, что бинарным отношением на множестве Х называется произвольное подмножество E Ì X ´ X.

Транзитивным называется отношение, удовлетворяющее следующему условию: если (x, y) Î E и (y, z) Î E, то (x, z) Î E для всех  x, y, z Î X. Отметим, что бинарное отношение можно однозначно представить орграфом G(X, E). Теперь для произвольного отношения Е определим новое отношение Е* следующим образом

E* = (x, y).

Легко проверить, что Е* - транзитивное отношение. Кроме того, Е* является наименьшим транзитивным отношением на Х в том смысле, что для произвольного транзитивного отношения F É E выполняется E* É F. Отно­ше­ние Е* называется транзитивным замыканием отношения Е.

Если отношение Е представить в виде графа G(X, E) в котором каждая дуга имеет вес 1, то транзитивное замыкание Е* можно вычислить с помощью алгоритма Флойда. При этом надо учесть, что

                                  (xi, xj) Î E* если .

Для большего удобства алгоритм Флойда в этом случае можно моди­фи­ци­ровать следующим образом.

Положим

                                    .

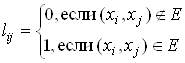Вместо (3) запишем

                                 ,

где    Ú – дизъюнкция (логическое сложение),

Ù – конъюнкция (логическое умножение).

После завершения работы алгоритма будем иметь

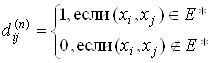
Модифицированный таким образом алгоритм называется алгоритмом Уоршелла.

ЛИТЕРАТУРА

1.  Баканович Э.А., Волорова Н.А., Епихин А.В. Дискретная математика:. В 2-х ч..– Мн.: БГУИР, 2000.– 52 с., ил. 14 ISBN 985-444-057-5 (ч. 2).

2.  Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. М. Иза-во МГТУ им. Н.Э.Баумана, 2003.

3.  Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).