Реферат: Разработка змееподобного робота, применяемого для диагностики трубопроводов
Реферат: Разработка змееподобного робота, применяемого для диагностики трубопроводов
Разработка змееподобного робота, применяемого для диагностики трубопроводов
Реалиями сегодняшнего дня в России являются устаревшие системы магистральных нефтегазопроводов. В настоящее время общая протяженность магистральных трубопроводов превышает 300 тыс. км. При этом около 40% газопроводов и 60% нефтепроводов находится в эксплуатации более 20 лет. Очевидно, что традиционный подход к поддержанию работоспособности трубопроводов путем проведения капитальных ремонтов отдельных участков труб не может обеспечить надежность и безопасность магистральных нефтегазопроводов из-за их большой протяженности и различного состояния. Поэтому, основной стратегией обеспечения высокой надежности магистральных систем становится эксплуатация и ремонт «по фактическому состоянию», то есть переход к выборочному «точечному» ремонту элементов и участков по результатам 100% диагностического обследования многокилометровых трубопроводов. В последние годы всё большее значение приобретает метод бестраншейной инспекции и ремонта трубопроводов с помощью роботов, одной из актуальных задач в этом направлении является создание змеевидного мобильного робота. Область возможного применения подобного робота необычайно широка. Это и подвижные управляемые извне макеты змей, используемые в киноиндустрии и индустрии развлечений, и специализированные роботы, предназначенные для выполнения исследовательских, инспекционных и спасательных работ в экстремальных условиях и чрезвычайных ситуациях на Земле и в планируемых экспедициях на другие планеты.
Бионический подход в разработке автоматизированных автономных устройств используется в робототехнике с первых шагов её развития. Можно сказать, многообразие живого мира, способности адаптации отдельных организмов к среде обитания и выполнению специальных операций, энергетическая экономичность при локомоциях, оснащенность средствами сенсорики и коммуникации, побуждают инженеров вступать в соревнование с природой. Одно из интересных направлений развития робототехники связано с разработкой змееподобных роботов. Биологические змеи распространены по всей планете, а способы передвижения и физиология этих существ делают их в высшей степени приспособленными к обитанию в средах с различными климатическими условиями. Змеевидное устройство, способное скользить, плавно передвигаться и перекатываться, перемещаясь по плохо структурированным поверхностям, в подвижных (сыпучих и жидких) средах, перемещаться в ограниченных областях, рассматривается как эффективная альтернатива традиционному шагающему или колесному роботу. Для выполнения змееподобных движений механическая система должна обладать числом степеней свободы, превосходящих число степеней традиционных манипуляторов, поэтому змеевидные роботы вместе с хоботообразными манипуляторами относятся к классу гиперизбыточных роботов.
В работе было проведено исследование двадцатизвенной бесколесной модели. Поиск программных движений строился на основе стохастических, генетических и нейронных алгоритмов. Были получены режимы движения, сходные с наблюдаемыми у пресмыкающихся, и новые, не зафиксированные в живой природе. Следует отметить, что трудности организации целенаправленного перемещения бесколесного змеевидного робота в значительной мере были связаны с отсутствием рациональной механической модели перемещения гибкого змеевидного тела.
После подбора и анализа различной информации удалось:
· выбрать модель исследования (в нашем случае модель робота);
· определить область применения исследуемого робота;
· определить основные модели организации движения робота с помощью виртуальной модели, и оценить их недостатки и преимущества;
· подобрать систему датчиков, с помощью которых возможна необходимая диагностика трубопроводов;
· проанализировать механику змеевидного манипулятора.

Рис. 1. Принципиальная конструкция модуля змеевидного робота
На основе виртуальной модели проведено исследование локомоций змеевидного робота. Показано, что применение зависимости (1) – (2) для шарнирных углов позволяет организовать целенаправленное предсказуемое движение дискретной модели.
![]() sin
sin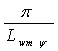 cos
cos![]() ,
,
![]() sin
sin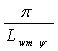 cos(
cos(![]() +2
+2![]() ).
).
Рассматриваемые роботы с диагностическими датчиками на борту, предназначены для движения внутри труб малых диаметров, в диапазоне от нескольких миллиметров до десятков сантиметров. С целью выполнения технической диагностики машин и агрегатов нефтехимической и газовой промышленности, энергетических объектов, проведения регламентных и ремонтных работ трубопроводов малых диаметров, а также применения в технологических процессах высокоточной обработки изделий для энергетических систем.
Приведенные в работе датчики могут входить в состав систем управления роботами для обеспечения высокоточных движений. Бортовые телекамеры необходимы для получения визуальной информации о состоянии внутренних поверхностей труб. Эта информация затем подвергается микропроцессорной обработке. В качестве диагностических устройств могут применяться микродатчики, построенные на иных принципах, например, ультразвуковые – для выявления внутренних трещин, электромагнитные и другие, реализующие методы неразрушающего контроля.
Реализация микропроцессорного управления движением миниатюрных роботов внутри труб малых диаметров представляет собой сложную научно-техническую задачу в связи с малыми размерами изделий и ограниченным пространством, в котором происходит движение. Это обуславливает необходимость повышения автономности управления и учета особенностей миниатюризации конструкции и специфики принципа действия механической системы робота. Существует большое многообразие способов движения тел по горизонтальной поверхности. Рассмотрим эти движения в предположении, что реактивные силы отсутствуют, а из внешних сил, действующих на тело, существенны лишь сила тяжести и сила реакции поверхности. Как известно, в этом случае существенную роль играют силы трения: при их отсутствии центр тяжести тела остается на месте. Примем, что на тело действуют силы сухого трения, подчиняющиеся закону Кулона.
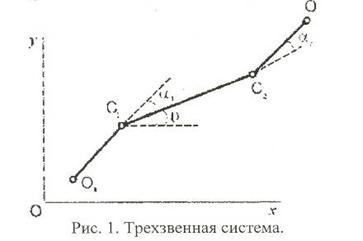
Рассмотрим сначала плоский трехзвенник О1С1С202 (Рис – 1), состоящий из центрального звена С1С2 длины 2а и двух звеньев О1С1 и С202 длины ℓ каждое. Многозвенник может двигаться по неподвижной шероховатой горизонтальной плоскости, в которой введена декартова система координат ху. Обозначим через х, у декартовы координаты середины корпуса, а через Θ1, Θ, Θ2 углы наклона звеньев О1С1, С1С2, С2О2 соответственно к оси х. Положим Θi = Θ + αi, где αi – углы между корпусом и концевыми звеньями ОiСi соответственно.
Между точками Оi, Сi, i=1,2 и плоскостью действуют силы сухого трения, подчиняющиеся закону Кулона. В состоянии движения сила трения направлена против скорости точки и равна тigk, где тi – масса точки, g – ускорение силы тяжести, k – кинематический коэффициент трения.
В шарнирах С1, C2 действуют управляющие моменты М1 и М2, которые могут изменяться произвольным заданным образом.
Чтобы получить любое заданное перемещение многозвенника по плоскости, достаточно построить его движения вдоль самого себя (продольное движение), поперек (боковое движение), а также вращение на месте. Эти движения сформируем из более простых движений, которые будем называть элементарными. Каждое элементарное движение начинается и заканчивается в состоянии покоя всего многозвенника. Элементарные движения делятся на медленные и быстрые. В медленных движениях вращается одно или оба концевых звена, а корпус остается неподвижным. Примем, что угловая скорость άi, i=1,2, концевых звеньев в медленном движении не меняет знака и справедливы соотношения
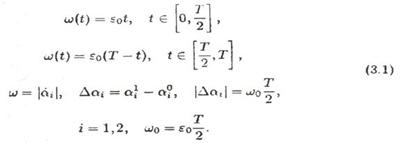
Здесь t – время, Т – длительность медленного движения, ω0 и ε0 - постоянные. Если в медленном движении участвуют оба концевых звена, то они вращаются синхронно, либо в одном и том же, либо в противоположных направлениях, так что
α2(t) = ±α1(t) + β, t є [0, T], (3.2)
где β – постоянная.
Можно показать [8], что при медленном движении одного или двух концевых звеньев корпус остаётся неподвижным, если
![]()
Если же концевые звенья вращаются в противоположные стороны, т.е. имеет место знак «–» в (3.2), то (3.3) может быть заменено условием
m0ℓ(ω04 + ε02)1/2 ≤ m1gk (3.4)
Если концевые звенья вращаются достаточно медленно, т.е. ω0 и ε0 в (3.1) достаточно малы, то неравенство (3.4) выполняется всегда, а неравенство (3.3) – при т0ℓ<т1а.
В быстрых движениях угловые скорости и ускорения достаточно велики, а время движения t мало по сравнению с временем T медленных движений.
При этом для трехзвенника, управляющие моменты М1 и М2 по величине много больше моментов сил трения, равных μgkL, где μ = тах(т0, т1), L=тах (ℓ, а), и поэтому силы трения можно не учитывать.
Здесь по-прежнему выполняется условие (3.2), причем имеет место один из трех случаев: 1) а2(t)=-а1(t)+β и, кроме того, либо а10=0, либо а20=0. 2) а2(t) = – а1(t) 3) а2(t)= а1(t). Эти случаи будем называть быстрыми движениями типов 1, 2, 3 соответственно. Закон изменения угловых скоростей в быстрых движениях несуществен.
Используя законы сохранения импульса и момента импульса, нетрудно подсчитать приращения за время быстрых движений линейных и угловых координат, определяющих положение и конфигурацию многозвенников.
В случае трехзвенника приращения переменных х, у, Θ для быстрого движения типа 1 равны
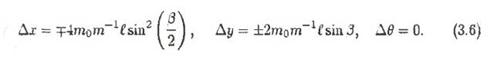
Здесь верхний и нижний знаки отвечают случаям а10=0 и а20=0 соответственно. Для быстрого движения типа 2 получим
![]()
Для быстрого движения типа 3 имеем Δх=Δу=0, ΔΘ≠0, причем для ΔΘ также получено явное выражение.
Перейдем к формированию продольного, бокового и вращательного движений многозвенников из элементарных движений.
Продольное движение. Пусть в начальный момент времени трехзвенник имеет прямолинейную форму (Θ=α1=α2=0) и покоится.
1) Выполним медленное движение, повернув звено О1C1 на угол β. Остальные звенья остаются неподвижны. Трехзвенник перейдет в состояние 1 на рис. 3, в котором α1 = β, α2=0
2) Выполним быстрое движение типа 1, в результате которого α1 изменится от β до 0, а α2 - от 0 до β. Трехзвенник перейдет в состояние 2 на рис. 3.
3) Выполним медленное движение, при котором α1 изменится от 0 до –β, а α2 – от β до 0. Трехзвенник перейдет в состояние 3 на рис. 3.
4) Выполним быстрое движение типа 1, при котором α1 изменится от -β до 0, а α2 – от 0 до -β. Трехзвенник перейдет в состояние 4 на рис. 3.
5) Выполним медленное движение, при котором α1 изменится от 0 до β, а α2 – от -β до 0. Трехзвенник перейдет в состояние 5 на рис. 3.
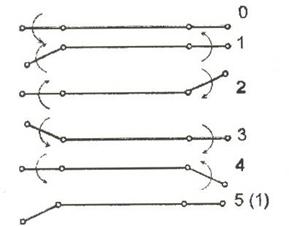
Рис. 3. Продольное движение трехзвенника
Состояние 5 тождественно состоянию 1. Описанный цикл из двух быстрых и двух медленных движений можно повторить любое число раз. Чтобы в конце движения перевести трехзвенник из состояния 5 в прямолинейное состояние 0, нужно выполнить медленное движение, изменив α1 от β до 0.
Подсчитаем полное перемещение трехзвенника за цикл движения. Так как для обоих быстрых движений цикла имеем α20 = 0, то в формулах (3.6) нужно брать нижние знаки, причем β для этих движений имеет разные знаки. Получим для полного смещения
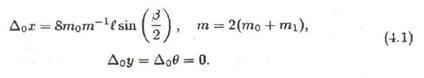
Средняя скорость продольного движения равна υ1 = Δ0 х(2Т)-1, где время медленного движения T и угол β должны удовлетворять неравенству
![]()
вытекающему из (3.1) и (3.3).
Теперь рассмотрим боковое движение. Начинаем движение снова из состояния покоя 0 см. рис. 4.
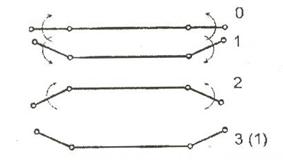
Рис. 4. Боковое движение трехзвенника
1) Выполним медленное движение, изменив угол α1 от 0 до -β, а а2 – от 0 до β. Трехзвенник перейдет в состояние 1 на рис. 4.
2) Выполним быстрое движение типа 2, изменив угол α1 от -β до β, а α2 – от β до -β. Трехзвенник перейдет в состояние 2 на рис. 4.
3) Выполним медленное движение, изменив угол α1 от β до -β, а α2 – от -β до β. Трехзвенник перейдет в состояние 3 на рис. 4.
Состояние 3 идентично состоянию 1. Цикл из быстрого и медленного движений можно повторять. Чтобы в конце движения привести трехзвенник из состояния 3 в исходное состояние 0, достаточно выполнить медленное движение, изменив α1 от -β до 0, а α2 – от β до 0.
Полное смещение трехзвенника за цикл определяется при помощи формул (3.7). Имеем
![]()
Средняя скорость бокового движения равна υ2=ΔоуТ-1, где время медленного движения Т и угол β должны удовлетворять неравенству
![]()
вытекающему из (3.1) и (3.4).
Чтобы повернуть трехзвенник, находящийся первоначально в состоянии 0 на рис. 5, выполним следующие движения (здесь всегда α1≡ α2).
1) При помощи медленного движения изменим α1= α2 от 0 до α°.
Трехзвенник перейдет в состояние 1 на рис. 5.
2) При помощи быстрого движения типа 3 изменим α1= α2 от α0 до α1. При этом корпус повернется на угол ΔΘ, трехзвенник перейдет в состояние 2 на рис. 5.
Данные движения можно повторять. Чтобы из состояния 2 привести трехзвенник в прямолинейное состояние, нужно выполнить медленное движение, изменив α1= α2 от α1 до 0. В результате трехзвенник повернется на месте на угол ΔΘ.
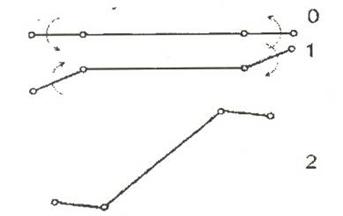
Рис. 5. Поворот трехзвенника.
Выводы
Как показано, плоский многозвенник может перемещаться по шероховатой горизонтальной плоскости в любом направлении, а также поворачиваться под действием внутренних управляющих моментов, приложенных к его шарнирам. Предложены простые конструктивные способы этих движений, даны достаточные условия их осуществимости, оценены смещения и скорости. Отметим отличительные особенности рассмотренного способа движения по сравнению с другими способами перемещения аппаратов и животных, использующими колеса, ноги, гусеницы.
Рассматриваемые движения происходят исключительно в горизонтальной плоскости, тело контактирует с плоскостью все время одними и теми же своими точками. Все точки тела движутся параллельно этой плоскости, а управляющие моменты перпендикулярны ей. Поэтому размеры тела по вертикали (высота аппарата) могут быть малыми. Высота же колесного или шагающего аппарата ограничена снизу размерами колес или ног.
Для реализации произвольных движений достаточно двух или даже одного двигателя, установленных в шарнирах (для шагающего аппарата требуется не менее двух двигателей для каждой ноги).
Конструкция аппарата и способ движения весьма просты. Эти особенности могут быть полезны при создании мобильных роботов малых размеров.
Список источников
1. Зенкевич С.Л., «Моделирование движения мобильного колесного робота по сложному маршруту», издательство Московского университета, 2000 г.
2. Мартыненко Ю.Г., «Проблема управления и динамика мобильных роботов», Новости искусственного интеллекта, 2002 г., №4 (52).
3. Сайт: www.robot.com.
Перепечатка материалов без ссылки на наш сайт запрещена