Учебное пособие: Четырехполюсники, электрические фильтры
Учебное пособие: Четырехполюсники, электрические фильтры
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(государственный технический университет)
ФИЛИАЛ «ВЗЛЕТ»
Кафедра РЭВС
РАЛДЫГИН И.К.
КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ
«Основы теории цепей». Часть 2.
Четырехполюсники, электрические фильтры.
Учебное пособие для студентов радиотехнической специальности.
|
Ахтубинск – 2003
Предисловие ко 2-й части
Во второй части конспекта по Основам теории цепей (ОТЦ) кратко изложена теория четырехполюсников (4х-П) и более подробно изложена теория электрических фильтров.
Анализ и синтез простейших электрических фильтров проводится с применением прикладной программы Mathcad 2000 (МС). Все расчеты, выполненные в среде Mathcad, проверены путем электронного моделирования по программе Electronics Workbench. Конспект, с его многочисленными примерами, может быть использован студентами при проектировании электрических фильтров на этапах разработки курсовых и дипломных проектов.
Работа написана на основе 4-х-летнего опыта применения упомянутых программ в учебном процессе.
Глава 1. Четырехполюсники
1.1 Основные определения и классификация четырехполюсников (4х-П)
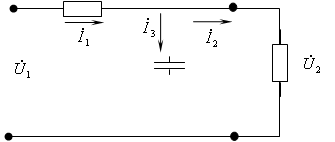
Часть электрической цепи, рассматриваемая по отношению к любым двум парам ее зажимов, называется 4х-П, Рис.1.1.

1
1’
Рис.1.1. Схема 4х-П. Его токи и напряжения.
Понятием 4х-П пользуются тогда, когда интересуются токами и напряжениями на входе «1-1’» и на выходе «2-2’».
В качестве 4х-П могут быть представлены: трансформатор, выпрямитель, электрический фильтр и другие устройства с двумя парами зажимов.
Четырехполюсники делятся на активные и пассивные. В составе активных 4х-П имеются источники энергии. Пассивные 4х-П не содержат источников энергии.
Четырехполюсники делятся на линейные и нелинейные. Если в состав 4х-П входит хотя бы один нелинейный элемент, то такой4х-П называется нелинейным. В данной работе рассматриваются только линейные 4х-П.
По схеме внутренних соединений различают Г-образные, Т-образные, П-образные и другие 4х-П, Рис.1.2.

Рис.1.2. Электрические схемы 4х-П.
Основной смысл теории 4х-П заключается в том, что, пользуясь некоторыми обобщенными параметрами, можно находить ток и напряжение на выходе 4х-П, не производя расчетов токов и напряжений внутри заданной схемы.
1.2 Системы уравнений четырехполюсников
Уравнениями 4х-П называют комплексные уравнения, связывающие комплексные действующие значения токов и напряжений на его входе и выходе.
Линейный пассивный 4х-П, естественно, описывается линейными уравнениями.
Из четырех величин ![]() характеризующих 4х-П, две
должны быть заданы, а две другие определяются из уравнения 4х-П. Всего, таким
образом, может быть составлено шесть форм записи уравнений.
характеризующих 4х-П, две
должны быть заданы, а две другие определяются из уравнения 4х-П. Всего, таким
образом, может быть составлено шесть форм записи уравнений.
Если 4х-П выполняет роль передаточного звена между источником и приемником электрической энергии, то обычно пользуются уравнениями в форме А:
|
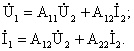
В этих уравнениях А11, А12, А21, А22 называются коэффициентами формы А. Они, в общем случае, являются комплексными числами, модули которых зависят от частоты.
Физический смысл коэффициентов формы А можно пояснить, если мысленно выполнить опыты холостого хода и короткого замыкания.
![]() В режиме
холостого хода
В режиме
холостого хода ![]() . Уравнение
(1.1.) принимает следующий вид:
. Уравнение
(1.1.) принимает следующий вид:
Отсюда получаем:
![]()
- отношение входного напряжения к выходному в режиме холостого хода;
![]()
- передаточная проводимость в режиме холостого хода.
В режиме короткого
замыкания ![]() . Уравнения (1.1) принимают
вид:
. Уравнения (1.1) принимают
вид:
![]()
Отсюда получаем:
![]()
- передаточное сопротивление в режиме короткого замыкания;
![]()
- отношение тока на входе к току на выходе в режиме короткого замыкания.
|
![]()
Из этого уравнения следует, что для составления системы (1.1) в форме А необходимо и достаточно определить только любые три коэффициента. Четвертый коэффициент определяется из (1.2).
Рассмотрим Г-образный 4х-П, изображенный на Рис.1.3, и определим для него коэффициенты формы А.

1 2
|
1’ 2’
Рис.1.3. Схема Г-образного 4х-П.
При определении коэффициентов формы А будем считать, что комплексные сопротивления Z1 и Z2 заданы.
Проведем опыт холостого
хода: зажимы 2-2’ - разомкнуты, ![]()
В этом случае ток на входе и напряжение на выходе определяются по закону Ома в комплексной форме:
![]()
![]() Эти
выражения можно записать так:
Эти
выражения можно записать так:
Отсюда получаем значения А11 и А21, выраженные через сопротивления Z1 и Z2:
![]()
Теперь проведем опыт
короткого замыкания: зажимы 2-2’ закорочены, ![]()
При этом в цепи осталось только одно сопротивление Z1 и, следовательно:
![]()
Таким образом, коэффициенты формы А Г-образного 4х-П можно представить в виде следующей матрицы
|
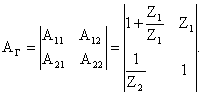
Аналогичным образом можно получить матрицу коэффициентов формы А для Т-образного4х-П:
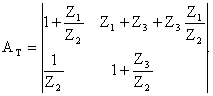
|
Кроме формы А (1,1) существуют еще пять форм записи уравнений 4х-П. Приведем еще две формы.
Форма Z.
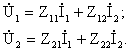
Форма Y.
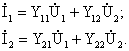
Полный перечень форм записи уравнений 4х-П приводится в учебниках, задачниках и справочниках по ОТЦ.
Если известны коэффициенты хотя бы одной формы записи уравнений 4х-П, то можно найти коэффициенты любой другой формы, решив систему уравнений, например (1,1) относительно искомых токов или напряжений.
1.3 Входное сопротивление, сопротивления холостого хода и короткого замыкания
Рассмотрим произвольный 4х-П с известными коэффициентами формы А, который нагружен активным сопротивлением R, Рис.1.4.

1
R
1’
Рис.1.4. Схема 4х-П, нагруженного активным сопротивлением R
Определим входное сопротивление 4х-П Рис.1.4., т.е. сопротивление со стороны зажимов 1-1’.
По закону Ома в комплексной форме входное сопротивление есть отношение входного напряжения к входному току (1.1):
![]()
|
Полученное выражение входного сопротивления показывает, что 4х-П может быть применен для преобразования сопротивления между источником и приемником.
Сопротивление холостого
хода 4х-П представляет собой частный случай входного сопротивления (1.5) при ![]()
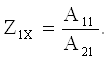
Сопротивление короткого
замыкания получается из (1.5) при ![]()
![]()
1.4 Передаточная функция четырехполюсника
При проектировании радиотехнических устройств широко применяются электрические фильтры, которые удобно рассматривать как 4х-П, предназначенные для передачи сигналов от входа к выходу с определенной избирательностью.
Передаточной функцией по напряжению называется отношение выходного напряжения к входному:
![]()
Модуль этого отношения представляет собой амплитудно-частотную характеристику (АЧХ), а аргумент – фазо-частотную характеристику (ФЧХ). Эти характеристики являются основными при выборе электрических фильтров.
Амплитудно-частотная характеристика показывает, во сколько раз выходное напряжение меньше (или больше) входного, ФЧХ дает сдвиг фаз между входным и выходным напряжениями.
Определим АЧХ и ФЧХ произвольного 4х-П с известными коэффициентами формы А, нагруженного активным сопротивлением R, Рис.1.4. С этой целью запишем первое уравнение системы (1.1) в следующем виде:
|
Поскольку коэффициенты формы А, в общем случае, являются комплексными числами, зависящими от частоты, постольку выражение в скобках (1.6) можно записать в алгебраической форме:
![]()
где а(ω) – действительная часть;
b(ω) – мнимая часть.
После этого связь входного и выходного напряжений (1.6) можно выразить следующим образом:
|
![]()
Для определения ФЧХ 4х-П
за начало отсчета сдвига фаз между входным и выходным напряжениями примем
вектор выходного напряжения ![]() ,
который направим по оси абсцисс, т.е. горизонтально.
,
который направим по оси абсцисс, т.е. горизонтально.
При таком выборе начала
отсчета положение вектора ![]() на
комплексной плоскости целиком определяется величинами а(ω)и b(ω) и их знаками:
на
комплексной плоскости целиком определяется величинами а(ω)и b(ω) и их знаками:

|
Расчет ФЧХ по (1.8) дает сдвиг фаз, выраженный в радианах. Ключ для определения этого угла показан на Рис.1.5:
![]() j
j
![]()
![]() φ
φ
![]() 0 +
0 +
![]()
-j
Рис.1.5. Ключ для определения сдвига фаз между входным и выходным напряжениями
На основании (1.7) комплексная передаточная функция по напряжению произвольного 4х-П с известными коэффициентами формы А и нагруженного активным сопротивлением R, принимает вид:
![]()
|
Модуль передаточной функции 4х-П, т.е. его АЧХ:
|
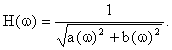
Таким образом, по формулам (1.8) и (1.10) можно рассчитать АЧХ и ФЧХ любого 4х-П при известных коэффициентах формы А и нагрузке R.
Пример 1.1. Задана электрическая схема Г-образного 4х-П (Рис.1.6) и его параметры R, L, C. Данный 4х-П подключен к источнику синусоидального напряжения. Необходимо найти формулы для расчета АЧХ и ФЧХ этого 4х-П.
L
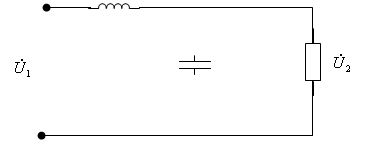
![]()
![]() 1 2
1 2
Z1
Z2 C R
![]()
1’ 2’
Рис.1.6. Электрическая схема г-образного 4х-П, нагруженного активным сопротивлением R
Решение. Комплексные сопротивления плеч 4х-П:
![]()
Коэффициенты формы А (1.3):
![]()
Комплексная передаточная функция:
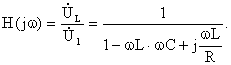
Модуль передаточной функции:
|
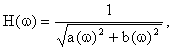
где ![]()
Фазо-частотная характеристика
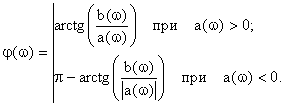
|
Таким образом, при известных значениях R, L, C-элементов по формулам (1.11), (1.12) можно рассчитать и построить графики АЧХ и ФЧХ Г-образного 4х-П, изображенного на Рис.1.6.
1.5 Каскадное соединение четырехполюсников
Рассмотрим так называемое каскадное соединение 4х-П (Рис.1.7), при котором входные зажимы каждого последующего 4х-П присоединяются к выходным зажимам предыдущего.

Рис.1.7. Каскадное соединение 4х-П
Эти два 4х-П, взятые вместе, можно рассматривать как один эквивалентный.
Определим параметры эквивалентного 4х-П через известные параметры первого и второго четырехполюсников.
Пусть заданы матрицы коэффициентов формы А двух каскадно соединенных 4х-П.
Из теории известно, что матрица коэффициентов формы А двух каскадно соединенных 4х-П равна произведению матриц отдельных 4х-П:
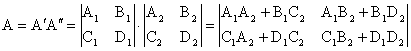
Это правило, распространяется на случай каскадного соединения любого числа 4х-П. При этом матрицы, подлежащие перемножению, записываются в порядке следования 4х-П, т.к. умножение матриц не подчиняется переместительному закону.
1.6 Одноэлементые четырехполюсники
Простейшими 4х-П являются одноэлементные 4х-П, состоящие из последовательного (Рис.1.8а) и параллельного (Рис.1.8б) двухполюсника.
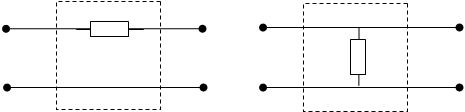
Z1 Z2
а) б)
Рис.1.8. Одноэлементный 4х-П
Матрицы коэффициентов формы А одноэлементных 4х-П:
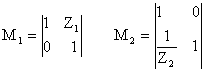
С помощью этих матриц М1 и М2 можно получить коэффициенты формы А любого 4х-П, построенного по лестничной схеме. Для этого необходимо перемножить матрицы М1 и М2 столько раз, сколько раз встречаются параллельный и последовательный 2х-П.
Например, коэффициенты формы А Г-образного 4х-П получаются после перемножения матриц М1 и М2 (см.1.3):
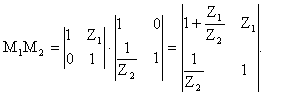
Глава 2. Электрические фильтры нижних частот
2.1 Основные определения и классификация электрических фильтров
Электрическим фильтром называется устройство, при помощи которого электрические колебания разных частот отделяются друг от друга. Электрический фильтр представляет собой пассивный 4х-П, пропускающий сигналы в некоторой полосе частот с малым затуханием, а за пределами этой полосы сигналы проходят в нагрузку с большим затуханием.
![]() Полоса
частот, в пределах которой передаточная функция по напряжению (1.10) принимает
не менее заданного значения
Полоса
частот, в пределах которой передаточная функция по напряжению (1.10) принимает
не менее заданного значения
называется полосой пропускания. Остальная область частот называется полосой задерживания. Частоты, разделяющие эти полосы, называются граничными.
В зависимости от пропускаемого спектра частот фильтры разделяются на:
l фильтры нижних частот (ФНЧ);
l фильтры верхних частот (ФВЧ);
l полосовые фильтры (ПФ);
l заграждающие фильтры (ЗФ).
В зависимости от электрической схемы фильтры разделяются на Г-образные, Т-образные, П-образные и другие.
В зависимости от числа реактивных элементов, входящих в состав фильтра, различают фильтры первого порядка, второго порядка и т.д.
По составу элементов фильтры делятся на активные и пассивные. Активные фильтры содержат источники электрической энергии, а пассивные их не содержат.
По способу обработки сигналов фильтры делятся на аналоговые и цифровые.
В данном курсе рассматриваются только пассивные электрические фильтры, построенные на идеальных линейных R, L, C-элементах.
2.2 Общий принцип действия линейных пассивных электрических фильтров
Рассмотрим электрический фильтр, частотные характеристики которого известны и описываются формулами (1.8)и (1.10).
Пусть на вход данного фильтра поступает сигнал в виде суммы различных частот
![]()
Определим структуру сигнала на выходе фильтра.
В силу линейности фильтра, сигнал на выходе будет также представлять сумму синусоидальных напряжений. При этом изменятся амплитуды и начальные фазы составляющих, а частоты составляющих на выходе фильтра одинаковы:
![]()
Амплитуды составляющих на выходе определяются передаточной функцией фильтра (1.10):
![]()
Сдвиг фаз между входным и выходным напряжениями определяется фазо-частотной характеристикой фильтра (1.8):
![]()
В дальнейшем будем полагать, что на вход фильтра подается синусоидальное напряжение, частота которого изменяется от нуля до бесконечности.
2.3 Общая характеристика фильтров нижних частот
Фильтры нижних частот (ФНЧ) предназначены для пропускания в нагрузку сигналов малой частоты и подавления сигналов большой частоты.
Полоса пропускания ФНЧ определяется его граничными частотами:
f1=0 – нижняя граница полосы пропускания;
f2 - верхняя граница полосы пропускания, которая определяется назначением данного конкретного фильтра.
В теории фильтров рассматриваются идеальные и реальные фильтры. Идеальным ФНЧ называется фильтр, передаточная функция которого (1.10) в полосе пропускания равна единице, а за пределами полосы пропускания она равна нулю:
![]()
Передаточная функция реального фильтра в полосе пропускания не равна единице, а в полосе задерживания - не равна нулю.
Передаточные функции по напряжению идеального и реального фильтров нижних частот показаны на Рис.2.1.
![]() H(f)
H(f)
![]()

 Передаточная функция
идеального ФНЧ
Передаточная функция
идеального ФНЧ
![]() Передаточная функция
реального ФНЧ
Передаточная функция
реального ФНЧ
![]() H1
H1
Полоса
пропускания Полоса задерживания
![]()
![]() H22
H22
![]() f2 f22
f
f2 f22
f
Рис.2.1. Передаточные функции идеального и реального фильтров нижних частот
Количественную оценку избирательности фильтра целесообразно производить с помощью коэффициента прямоугольности передаточной функции по напряжению или мощности.
Для расчета коэффициента прямоугольности передаточной функции фильтра введем в рассмотрение передаточную функцию по мощности, которую определим следующим образом.
Максимально возможная мощность, которая может быть выделена в нагрузке в случае идеального фильтра, определяется по формуле:
![]()
|
где U1 – действующее значение входного напряжения;
R – сопротивление нагрузки.
Фактическая мощность, выделяемая в нагрузке реального фильтра, определяется действующим значением выходного напряжения, которое зависит от частоты входного напряжения:
![]()
|
Передаточной функцией по мощности будем называть отношение мощности, выделяемой в нагрузке реального фильтра (2.2) к мощности, выделяемой в нагрузке, идеального фильтра:
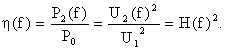
|
Таким образом, передаточная функция по мощности есть квадрат передаточной функции по напряжению (2.3).
Отметим, что в известных учебниках по ОТЦ частотные характеристики фильтров оцениваются затуханием, которое выражается в децибелах (дБ):
|
Из этой формулы следует, что фактически производится оценка затухания (ослабления) сигнала по мощности.
Поскольку физический смысл формулы (2.4) спрятан под знаком логарифма, постольку в дальнейшем будем пользоваться более простой формулой (2.3), физический смысл которой более прост и понятен.
Расчет коэффициента прямоугольности передаточной функции по мощности ФНЧ будем производить следующим образом.
Определим частоту, на которой передаточная функция по мощности составляет 5% от максимума:
![]()
За пределами этой частоты будем считать, что передаточная функция равна нулю
![]()
Определим полную площадь под кривой передаточной функции (Рис.2.1):
|
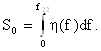
Определим также площадь
под кривой передаточной функции в пределах полосы пропускания (0…f2), где передаточная функция по напряжению ![]() а передаточная функция по
мощности
а передаточная функция по
мощности ![]() (Рис.2.1):
(Рис.2.1):
|
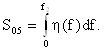
Коэффициентом прямоугольности передаточной функции по мощности будем называть отношение найденных площадей:
|
По физической сущности коэффициент прямоугольности представляет собой коэффициент полезного использования площади под кривой передаточной функции по мощности и дает представление о степени соответствия реального фильтра идеальному с той же полосой пропускания.
2.4 Емкостной фильтр нижних частот
2.4.1 Частотные характеристики емкостного фильтра нижних частот первого порядка (ФНЧ-1)
Рассмотрим электрическую схему, изображенную на Рис.2.3, которая представляет собой простейший фильтр нижних частот первого порядка (ФНЧ-1).
.
|
|
|
С R
1’ 2’
Рис.2.3. Емкостной фильтр нижних частот (ФНЧ-1)
![]() Работа
ФНЧ-1:
Работа
ФНЧ-1:
При
![]()
При
На малых частотах емкость
обладает большим сопротивлением и поэтому весь ![]() проходит
только через резисторы r, R, не ответвляясь в емкость.
проходит
только через резисторы r, R, не ответвляясь в емкость.
На больших частотах емкость обладает малым сопротивлением. Она закорачивает нагрузку и поэтому выходное напряжение мало.
Определим для этого фильтра АЧХ и ФЧХ, рассматривая его как Г-образный 4х-П, нагруженный активным сопротивлением R.
Сопротивления плеч фильтра:
![]()
Коэффициенты формы А:
![]()
Уравнение связи входного и выходного напряжений (1.6):
![]()
|
где ![]() - эквивалентное сопротивление
при параллельном соединении R и r.
- эквивалентное сопротивление
при параллельном соединении R и r.
|
![]()
Передаточные функции ФНЧ-1 принимают вид:
|
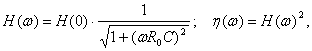
где ![]() - значение передаточной
функции на частоте ω=0.
- значение передаточной
функции на частоте ω=0.
Теперь, по формулам (2.9) и (2.10) можно, при известных значениях R, r, C-элементов, рассчитать и построить графики АЧХ и ФЧХ простейшего фильтра нижних частот (ФНЧ-1).
При изучении частотных характеристик фильтров удобно пользоваться АЧХ ФЧХ в параметрической форме. Для этого необходимо ввести в рассмотрение приведенную, или так называемую нормированную частоту, которая, в данном случае, определяется по формуле
|
где ![]() - граничная частота, на
которой реактивное сопротивление емкости равно активному сопротивлению
- граничная частота, на
которой реактивное сопротивление емкости равно активному сопротивлению ![]()
Запишем (2.9) и (2.10) в параметрической форме:
|
|
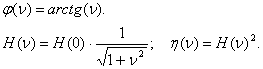
Параметрические функции (2.11) и (2.12) позволяют проводить общий анализ АЧХ и ФЧХ фильтра при заданных значениях R, r-элементах и произвольном значении емкости С.
Пример 2. Рассчитать и построить графики ![]() при следующих исходных
данных:
при следующих исходных
данных:
R=100 Ом – сопротивление нагрузки;
r=5 Ом – внутреннее сопротивление источника.
Оценить коэффициент прямоугольности передаточной функции по мощности.
Результаты расчетов представлены на Рис.2.4 и Рис.2.5.
Из этих рисунков видно, что передаточная функция по мощности при частоте ν=0 принимает значение H(0)=0,98, а затем плавно уменьшается с увеличением частоты. Коэффициент прямоугольности этой функции составляет всего П=0,545. Это означает, что данный фильтр соответствует идеальному фильтру на 54,5%.
Сдвиг фаз между входным и выходным напряжениями изменяется от 0 до 900. При этом выходное напряжение опережает входное.

2.4.2 Синтез емкостного фильтра нижних частот первого порядка
Синтез (проектирование) любого технического устройства начинается с разработки технического задания (ТЗ), в котором приводятся исходные данные и формулируются требования к устройству.
Применительно к ФНЧ-1 техническое задание на его проектирование можно изложить следующим образом:
1. Спроектировать емкостной фильтр нижних частот, схема которого приведена на Рис.3.2.
2. На вход фильтра подаются сигналы синусоидальной формы, частота которых изменяется от 0 до ∞.
3. Сопротивление нагрузки R, а внутреннее сопротивление источника r, (R>>r).
4. Передаточная функция по напряжению на нижней границе полосы пропускания (f1=0) должна принимать значение, близкое к единице, а на верхней границе f2 передаточная функция должна принимать значение H(f2)=H1.
5. Определить потребное значение емкости, рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности.
В условиях данной задачи неизвестной величиной является только емкость, которую достаточно просто можно найти из уравнения передаточной функции. Однако, в интересах общности изложения последующего материала воспользуемся передаточной функцией в параметрической форме (2.14), из которой найдем значение приведенной частоты n2, на которой передаточная функция (2.12) принимает заданное значение H1:
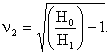
|
Очевидно, что (2.14) имеет смысл только при H1<H0.
Теперь формулу (2.11) можем записать в виде
![]()
откуда находим потребное значение емкости для построения ФНЧ-1 Рис.3.2:
![]()
|
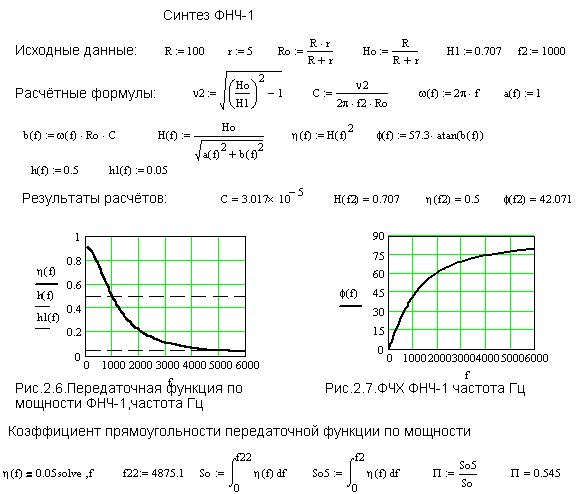
Пример 2.2. Спроектировать ФНЧ-1 Рис.2.3 при следующих исходных данных:
R=100 Ом – сопротивление нагрузки;
r=5 Ом – внутреннее сопротивление источника;
f2=1000 Гц – верхняя граница полосы пропускания;
H1=H(f2)=0,707 – значение передаточной функции на верхней границе полосы пропускания;
h1=h(f2)=0,5 - значение передаточной функции по мощности на верхней границе полосы пропускания.
Рассчитать АЧХ и ФЧХ фильтра, оценить коэффициент прямоугольности передаточной функции по мощности.
Результаты расчетов представлены на Рис.2.6 и Рис.2.7.
Из этих рисунков видно, что на верхней границе полосы пропускания f2=1000 Гц передаточная функция по мощности h(f2)=0,5, что соответствует требованиям технического задания.
Сдвиг фаз между входным и выходным напряжениями F(f2)=42,071 град. Коэффициент прямоугольности передаточной функции по мощности составляет П=0,545.
Потребное значение емкости для построения ФНЧ-1 Рис.3.2 составляет С=30,17 мкФ.
2.5 Г-образный фильтр нижних частот (ФНЧ-2)
2.5.1 Частотные характеристики ФНЧ-2
В целях повышения коэффициента прямоугольности передаточной функции по мощности применяют фильтры нижних частот второго порядка, в состав которых входят два реактивных элемента: L и C.
Рассмотрим Г-образный ФНЧ, схема которого представлена на Рис.2.8 (см.также Рис.1.6).
 L
L
![]()
Z1
Z2 C R
Рис.2.8. Электрическая схема Г-образного ФНЧ
Работа Г-образного ФНЧ:
![]()
при
![]() при
при
На малых частотах индуктивное сопротивление мало, а емкостное сопротивление велико, поэтому ток проходит в нагрузку с малым ослаблением, не ответвляясь в емкость.
На больших частотах индуктивное сопротивление велико, а емкостное сопротивление мало. Ток, прошедший через индуктивность, закорачивается емкостью. Поэтому выходное напряжение мало.
Определим АЧХ и ФЧХ Г-образного ФНЧ, рассматривая его как Г-образный 4х-П, нагруженный активным сопротивлением R.
Комплексные сопротивления плеч фильтра:
![]()
Коэффициенты формы А:
![]()
Уравнение связи входного и выходного напряжений (1.6) принимает вид:
![]()
|
Обозначим, как и ранее, действительную и мнимую части (2.16):
![]() - действительная часть;
- действительная часть;
![]() - мнимая часть.
- мнимая часть.
Уравнение (2.16) запишем в виде:
![]()
|
Фазочастотная характеристика ФНЧ-2 определяется по формуле:
|
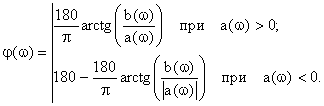
Комплексная передаточная функция по напряжению определяется из (2.17):
![]()
|
Модули передаточных функций по напряжению и мощности принимают вид:
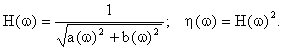
|
Таким образом, при известных значениях R, L, C-элементов, по формулам (2.18), (2.20) можно рассчитать и построить графики АЧХ и ФЧХ Г-образного ФНЧ.
С целью общего анализа частотных характеристик Г-образного ФНЧ представим передаточные функции (2.20) в параметрической форме, для чего обозначим:
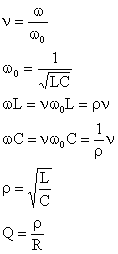
|
После подстановки обозначений в (2.20) получим передаточные функции в параметрической форме:
|
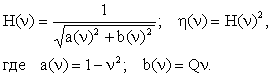
Пример 2.3. Рассчитать и построить семейство кривых передаточной функции по мощности в параметрической форме для трех значений коэффициента нагрузки:
![]()
Определить коэффициент
прямоугольности передаточной функции по мощности при ![]()
Расчет передаточной функции по мощности, выполненный по формуле (2.21) приведен на Рис.2.9.
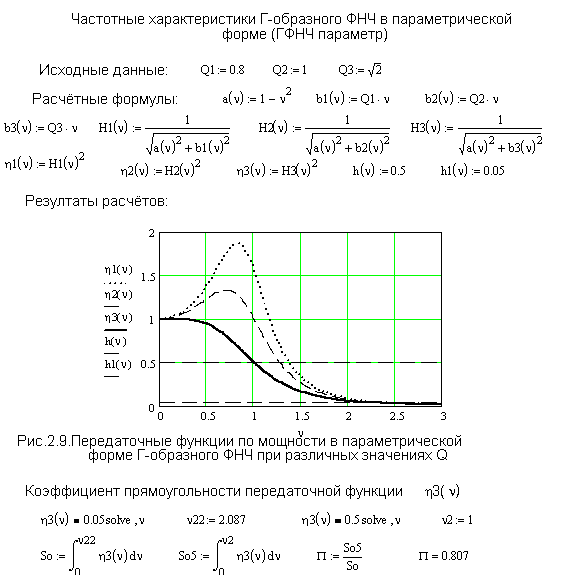
Из Рис.2.9 следует, что
при Q1=0,8 передаточная функция ![]() достигает
своего максимума, равного 1,86, а затем плавно уменьшается, Этот всплеск
передаточной функции может быть желательным или нежелательным в зависимости от
конкретного назначения фильтра.
достигает
своего максимума, равного 1,86, а затем плавно уменьшается, Этот всплеск
передаточной функции может быть желательным или нежелательным в зависимости от
конкретного назначения фильтра.
При Q2=1 всплеск передаточной функции ![]() значительно меньше и при
значительно меньше и при ![]() он вовсе отсутствует.
он вовсе отсутствует.
Таким образом, характер
изменения передаточной функции ![]() Г-образного
ФНЧ целиком определяется значением коэффициента нагрузки Q, который, в свою очередь, зависит от
комбинации значений RLC-элементов.
Следовательно, путем соответствующего выбора LC-элементов можно изменить форму кривой передаточной функции.
Г-образного
ФНЧ целиком определяется значением коэффициента нагрузки Q, который, в свою очередь, зависит от
комбинации значений RLC-элементов.
Следовательно, путем соответствующего выбора LC-элементов можно изменить форму кривой передаточной функции.
Коэффициент
прямоугольности передаточной функции по мощности при ![]() составляет П=0,807, что
значительно больше, чем у ФНЧ-1.
составляет П=0,807, что
значительно больше, чем у ФНЧ-1.
2.5.2 Синтез Г-образного фильтра нижних частот
Техническое задание на проектирование Г-образного ФНЧ формулируется следующим образом.
1. Спроектировать Г-образный ФНЧ, схема которого представлена на Рис.2.8.
2. На вход фильтра подаются сигналы синусоидальной формы, частота которых изменяется от нуля до бесконечности.
3.
Передаточные
функции по напряжению и мощности в полосе пропускания (0…f2), должны быть максимально плоскими, т.е. не иметь
всплесков, превышающих единицу, и на верхней границе полосы пропускания должны
принимать значения ![]() .
.
4. Сопротивление нагрузки чисто активное, равное R.
5. Рассчитать потребные значения индуктивности и емкости для построения фильтра. Построить графики АЧХ и ФЧХ, оценить коэффициент прямоугольности передаточной функции по мощности.
Порядок проведения расчетов состоит в следующем.
Из анализа ТЗ и формул
передаточных функций (2.20) следует, что при заданных значениях ![]() необходимо найти два
неизвестных параметра L и C, при которых фильтр будет
удовлетворять требованиям технического задания.
необходимо найти два
неизвестных параметра L и C, при которых фильтр будет
удовлетворять требованиям технического задания.
Другими словами, необходимо найти такие значения L, С-элементов, при которых передаточная функция H(w) проходит через точку на плоскости с координатами w2, H1.
Математически это означает, что для определения двух неизвестных необходимо составить два независимых уравнения и решить эту систему относительно L и С.
Для составления первого
уравнения необходимо из семейства кривых Рис.2.9 выбрать кривую, которая
соответствует требованиям ТЗ, и по ней при заданном значении ![]() найти значение приведенной
частоты n2.
найти значение приведенной
частоты n2.
В данном случае
требованиям ТЗ удовлетворяет передаточная функция ![]() ,
построенная при
,
построенная при ![]() .
.
Точное значение приведенной частоты определяется путем решения уравнения:
|
![]()
Результаты расчетов по
формуле (2.22) при ![]() приведены в таблице
2.1.
приведены в таблице
2.1.
Таблица 2.1.
|
H1 |
0.707 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
|
n2 |
1.0 | 1.55 | 1.316 | 1.513 | 1.783 | 2.213 | 3.154 |
Найденная приведенная
частота n2 связана с верхней границей полосы пропускания ![]() и неизвестной резонансной
частотой w0 следующим соотношением:
и неизвестной резонансной
частотой w0 следующим соотношением:
![]()
Отсюда получаем первое независимое уравнение для определения неизвестных LC-элементов
![]()
|
Выбранная кривая
передаточной функции ![]() построена при
построена при ![]() .
.
Следовательно, второе независимое уравнение можно записать в виде:
![]()
|
Совместное решение (2.23) и (2.24) дает формулы для определения неизвестных LC-элементов:
![]()
|
Теперь по формулам (2.18), (2.20), и (2.25) можно рассчитать потребные значения LC-элементов для построения Г-образного ФНЧ, а также рассчитать и построить графики АЧХ и ФЧХ этого спроектированного фильтра.
Пример 2.4. Спроектировать Г-образный ФНЧ, схема которого представлена на Рис.2.8:
Исходные данные:
R=100 Ом – сопротивление нагрузки;
f2=1000 Гц – верхняя граница полосы пропускания;
H(f2)=0,707 – значение передаточной функции по напряжению на верхней границе полосы пропускания.
Требование к фильтру: передаточные функции по напряжению и мощности в полосе пропускания должны быть максимально плоскими, т.е. не иметь всплесков и провалов.
Решение. Из Рис.2.9. выбираем кривую ![]() , которая удовлетворяет
требованиям технического задания.
, которая удовлетворяет
требованиям технического задания.
Из таблицы 2.1 по заданному значению Н1=Н(f2)=0,707 выбираем соответствующее значение приведенной частоты n2=1.
По формулам (2.25) определяем потребные значения LC-элементов для построения Г-образного ФНЧ.
По формулам (2.18) и (2.20) рассчитываем АЧХ и ФЧХ спроектированного фильтра и оцениваем коэффициент прямоугольности передаточной функции по мощности этого фильтра.
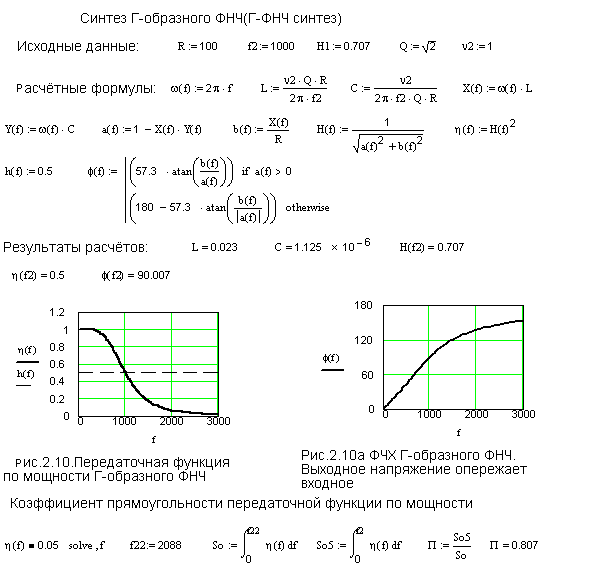
Результаты расчетов приведены на Рис.2.10 и Рис.2.10а.
Из этих результатов
главными являются найденные значения индуктивности и емкости: L=23 мГн и С=1,125 мкФ, при которых передаточные
функции на верхней границе полосы пропускания принимают заданные значения: ![]()
Следовательно, спроектированный Г-образный ФНЧ удовлетворяет требованиям технического задания.
Коэффициент прямоугольности передаточной функции по мощности Г-образного ФНЧ составляет П=0,807.
Отметим, что изложенный порядок проектирования носит общий характер и может применяться в среде Mathcad при любой комбинации исходных данных: H1, f2, R, Q.
2.6 Т-образный фильтр нижних частот
2.6.1 Частотные характеристики Т-образного фильтра нижних частот
В целях дальнейшего повышения коэффициента прямоугольности применяют фильтры третьего порядка, к числу которых относится Т-образный ФНЧ, изображенный на Рис.2.11.
 L1 L2
L1 L2
Z1 Z3
Z2 C R
Рис.2.11. Электрическая схема Т-образного ФНЧ
Работа Т-образного ФНЧ
На малых частотах индуктивные сопротивления Z1, Z3 малы, а емкостное сопротивление Z2 велико, поэтому ток проходит в нагрузку с малым ослаблением.
На больших частотах на пути тока в нагрузку стоят два больших сопротивления индуктивностей L1 и L2, а ток, прошедший через L1 закорачивается малым емкостным сопротивлением.
Определим АЧХ и ФЧХ Т-образного ФНЧ, рассматривая его как Т-образный 4х-П, нагруженный активным сопротивлением R.
Комплексные сопротивления плеч фильтра:
![]()
Коэффициенты формы А:

где - коэффициент
асимметрии фильтра, который может быть выбран в пределах ![]()
Уравнение связи входного и выходного напряжений:
|

Фазо-частотная характеристика фильтра определяется по формулам (1.8), а передаточная функция по напряжению рассчитывается по формуле (1.10).
Таким образом, при известных значениях RLC - элементов можно рассчитать и построить графики АЧХ и ФЧХ Т-образного ФНЧ, используя формулы (1.8), (1.10) и (2.26).
Представим, как и ранее для Г-образного ФНЧ, передаточные функции по напряжению и мощности в параметрической форме:
|
![]() Пример
2.5. Рассчитать
и построить семейство кривых передаточной функции по мощности в параметрической
форме (2.27) для трех значений коэффициента нагрузки:
Пример
2.5. Рассчитать
и построить семейство кривых передаточной функции по мощности в параметрической
форме (2.27) для трех значений коэффициента нагрузки:
Результаты расчетов представлены на Рис.2.12.
Из Рис.2.12 следует, что
для Т-образного несимметричного ФНЧ оптимальным значением коэффициента нагрузки
следует считать Q2=1,0 при коэффициенте асимметрии ![]() , который был определен в
результате предварительных исследований.
, который был определен в
результате предварительных исследований.
Коэффициент
прямоугольности передаточной функции по мощности Т-образного несимметричного
ФНЧ при Q=1 и ![]() равен
П=0,905.
равен
П=0,905.
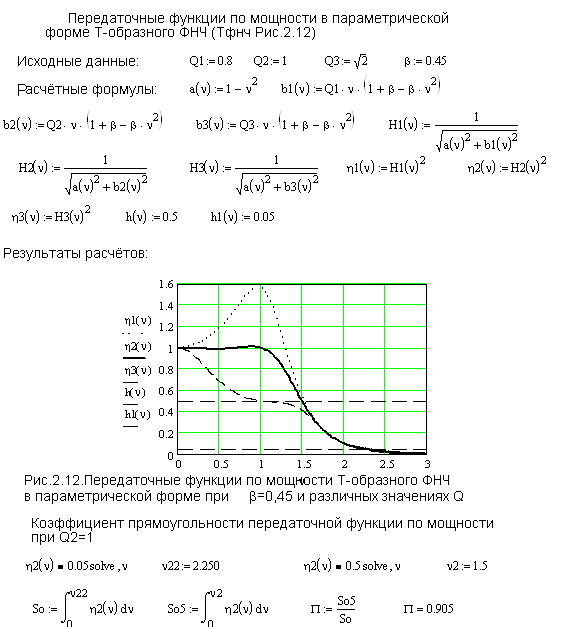
2.6.2. Синтез Т-образного фильтра нижних частот
Поставим задачу спроектировать Т-образный несимметричный ФНЧ по ТЗ на проектирование Г-образного ФНЧ.
Из Рис.2.11 видно, что в состав Т-образного фильтра входят три неизвестных реактивных элемента: L1, L2 и С, которые необходимо определить.
Следовательно, для определения трех неизвестных необходимо составить три независимых уравнения.
Порядок определения L1 и С аналогичен порядку определения этих элементов для Г-образного ФНЧ.
Из семейства кривых
Рис.2.12 выбираем кривую, которая удовлетворяет требованиям ТЗ. В данном случае
выбираем кривую ![]() которая построена
при Q2=1.
которая построена
при Q2=1.
После этого определяем значение приведенной частоты n2, на которой Н(n2)=Н1. Для этого решаем следующее уравнение:
![]()
в результате получим таблицу 2.2.
Таблица 2.2.
|
Н1 |
0,707 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 |
|
n2 |
1,5036 | 1,615 | 1,730 | 1,867 | 2,049 | 2,327 | 2,890 |
Далее, как и для Г-образного ФНЧ, можем записать два уравнения для определения L1 и С:
Совместное решение этих уравнений дает формулы для определения L1 и С:
![]()
|
Значение второй индуктивности L2 определяется из условия выбранного коэффициента асимметрии
|
![]()
Пример 2.6. Спроектировать Т-образный ФНЧ, схема которого показана на Рис.2.11.
Исходные данные:
R=100 Ом – сопротивление нагрузки;
f2=1000 Гц – верхняя граница полосы пропускания;
H1=H(f2)=0,707 – значение передаточной функции по напряжению на верхней границе полосы пропускания.
Передаточные функции H(f) и h(f) в полосе пропускания не должны иметь всплесков и провалов.
Решение. Из таблицы 2.2 по заданному значению H1=H(f2)=0,707 при Q=1 выбираем значение приведенной частоты n2=1,5036.
Потребные значения индуктивностей и емкости определяем по (2.28), (2.29).
Расчет передаточной функции по мощности проведем по формуле (1.10), ФЧХ – по формуле (1.8) с учетом (2.26).
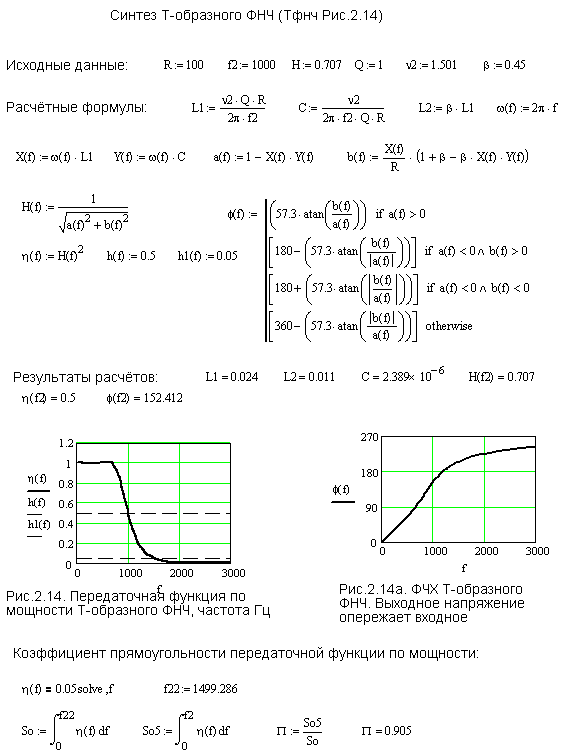
Результаты расчетов представлены на Рис.2.14, Рис.2.14а.
Из этого рисунка видно, что потребные значения индуктивностей и емкости для построения несимметричного Т-образного ФНЧ составляют: L1=24мГн, L2=11 мГн, C=2,389 мкФ.
Передаточные функции на верхней границе полосы пропускания принимают значения: Н(f2)=0,707, h(f2)=0,5, что и требовалось по техническому заданию.
Коэффициент прямоугольности передаточной функции по мощности составляет П=0,905.
Перепечатка материалов без ссылки на наш сайт запрещена